题目内容
15. 如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积36.
如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积36.
分析 根据勾股定理求出BD,根据勾股定理的逆定理求出△ABD是直角三角形,分别求出△ABD和△BCD的面积,即可得出答案.
解答 解:在△ABD中,
∵∠A=90°,AD=3,AB=4,
∴BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=5,
S△ABD=$\frac{1}{2}$AB•AD=$\frac{1}{2}$×4×3=6,
在△BCD中,
∵BC=12,CD=13,BD=5,
∴BD2+BC2=CD2,
∴△CBD是直角三角形,
∴S△CBD=$\frac{1}{2}$BC•BD=$\frac{1}{2}$×12×5=30.
∴四边形ABCD的面积=S△ABD+S△BCD=6+30=36.
故答案为:36.
点评 本题考查了勾股定理,勾股定理的逆定理的应用,解此题的关键是能求出△ABD和△BCD的面积,注意:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
17.“高斯”被誉为“数学王子”,他在10岁时就巧算出1+2+3+…+100=5050,他教会了我们要学会思考,亲爱的同学,你能象高斯那样快速计算出4+6+8+10+…+202=( )
| A. | 10100 | B. | 10200 | C. | 10300 | D. | 10400 |
 现有一个“Z”型的工件(工件厚度忽略不计),如图示,其中AB为20cm,BC为60cm,∠ABC=90°,∠BCD=50°,求该工件如图摆放时的高度(即A到CD的距离).
现有一个“Z”型的工件(工件厚度忽略不计),如图示,其中AB为20cm,BC为60cm,∠ABC=90°,∠BCD=50°,求该工件如图摆放时的高度(即A到CD的距离). 如图,四边形ABCD中,AB=6,BC=4,AD=2,CD=6,且∠B=∠D=60°.则四边形ABCD的面积为9$\sqrt{3}$.
如图,四边形ABCD中,AB=6,BC=4,AD=2,CD=6,且∠B=∠D=60°.则四边形ABCD的面积为9$\sqrt{3}$. 如图,△ABC中,AD、AE分别是BC边上的中线和高,点F是AB中点,作FH⊥BC于点H,FH与AD的延长线交于点G.若AC=$\sqrt{34}$,tan∠ABC=$\frac{4}{5}$,DE=FH,则HG=$\sqrt{2}$.
如图,△ABC中,AD、AE分别是BC边上的中线和高,点F是AB中点,作FH⊥BC于点H,FH与AD的延长线交于点G.若AC=$\sqrt{34}$,tan∠ABC=$\frac{4}{5}$,DE=FH,则HG=$\sqrt{2}$.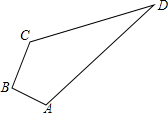 如图,四边形ABCD中,∠B=90°,AB=6,BC=8,CD=24,AD=26,求四边形ABCD的面积.
如图,四边形ABCD中,∠B=90°,AB=6,BC=8,CD=24,AD=26,求四边形ABCD的面积.