题目内容
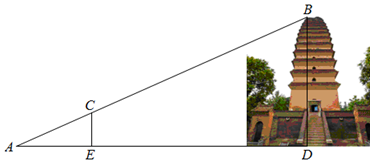
4.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交BC于E,交CD于F,EG⊥AB于G.(1)如图1,求证:CF=EG;
(2)如图2,当tan∠EAB=$\frac{1}{2}$,EF=$\sqrt{5}$时,求四边形CFGE的面积.

分析 (1)根据角平分线的性质,可得EC=EG,易证△CEF是等腰三角形,即可得CF=CE=EG,由此即可解决问题.
(2)首先证明四边形CFGE是菱形,再证明∠1=∠4=∠3,推出tan∠1=$\frac{EO}{CO}$=$\frac{1}{2}$,由OE=OF=$\frac{\sqrt{5}}{2}$,推出OC=OG=$\sqrt{5}$,根据菱形的面积公式计算即可解决问题.
解答 (1)证明:如图1中,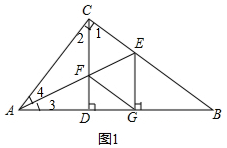
∵在Rt△ABC中,∠ACB=90°,
∴AC⊥CE,
∵AE平分∠BAC,EG⊥AB,
∴∠3=∠4,EC=EG,
∵CD⊥AB,
∴CD∥EG,∠CFE=∠AFD=90°-∠3,
∵∠AEC=90°-∠3,
∴∠CFE=∠CEF,
∴CF=CE,
∴CF=EG,
(2)解:如图2中,连接CG交AE于O.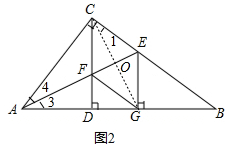
由(1)可知,CF=EG,CF∥EG,
∴四边形CFGE是平行四边形,
∵CF=CE,
∴四边形CFGE是菱形,
∴CG⊥AE,
∵∠1+∠CEO=90°,∠4+∠CEO=90°,
∴∠1=∠4=∠3,
∵tan∠3=$\frac{1}{2}$,
∴tan∠1=$\frac{EO}{CO}$=$\frac{1}{2}$,∵OE=OF=$\frac{\sqrt{5}}{2}$,
∴OC=OG=$\sqrt{5}$,
∴四边形CFGE的面积=$\frac{1}{2}$•CG•EF=$\frac{1}{2}$•2$\sqrt{5}$•$\sqrt{5}$=5.
点评 此题考查了菱形的判定和性质、等腰三角形的判定与性质、平行四边形的判定、锐角三角函数、角平分线的性质定理等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6. 已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是( )
已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是( )
 已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是( )
已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是( )| A. | m>0,n<3 | B. | m<0,n>3 | C. | m<0,n<3 | D. | m>0,n>3 |
9. 如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
 如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.| A. | 16-8$\sqrt{3}$ | B. | -12+8$\sqrt{3}$ | C. | 8-4$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
 如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积36.
如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积36. 在△ABC中,AC=BC,BD⊥AC,交AC边的延长线于点D,点E在AB边上,EF⊥BD于点F,且EF=BD,若AC=$\frac{13}{4}$,DF=1(BF>CD),则线段BE的长为$\sqrt{13}$.
在△ABC中,AC=BC,BD⊥AC,交AC边的延长线于点D,点E在AB边上,EF⊥BD于点F,且EF=BD,若AC=$\frac{13}{4}$,DF=1(BF>CD),则线段BE的长为$\sqrt{13}$.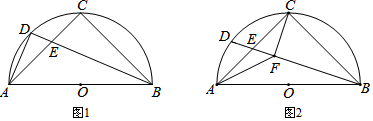
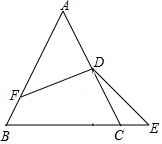 已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$.
已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$.