题目内容
9.在平面直角坐标系中,AC为∠BAO的角平分线,CD∥AB,且CD平分∠ACO.(1)求∠B的大小;
(2)点E为第二象限内一动点,若∠AEO,∠ABO的平分线相交于点F,且∠EFB=20°,问:
①∠EOB-∠BAE不变;②∠EOB+∠BAE不变,选择①,②中正确的结论证明.
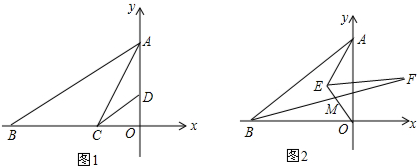
分析 (1)AC为∠BAO的角平分线,CD平分∠ACO,得到∠OAC=∠CAB=$\frac{1}{2}$∠OAB,∠ACD=∠OCD=$\frac{1}{2}$∠ACO,根据平行线的性质得到∠CAB=∠ACD,于是得到∠OCA=2∠ACD=∠OAB,根据三角形外角的性质即可得到结论;
(2)根据三角形的内角和和三角形外角的性质得到∠OEF=∠BOE+$\frac{1}{2}$∠ABO-∠EFB=∠BOE-5°,于是得到∠AEO=2∠OEF=2∠BOE=10°,推出∠AEO=∠ABO+∠BAE+∠BOE=30°+∠BAE+∠EOB,即可得到结论.
解答 (1)解:AC为∠BAO的角平分线,CD平分∠ACO,
∴∠OAC=∠CAB=$\frac{1}{2}$∠OAB,∠ACD=∠OCD=$\frac{1}{2}$∠ACO,
∵CD∥AB,
∴∠CAB=∠ACD,
∴∠OCA=2∠ACD=∠OAB,
∵∠OCA=∠CAB+∠B,
∴∠B=$\frac{1}{2}$∠OAB,
∵∠B+∠OAB=90°,
∴∠B=30°;
(2)解:①∠EOB-∠BAE不变是正确的;理由如下:
∵∠AEO,∠ABO的平分线相交于点F,
∴∠OEF=∠BOE+$\frac{1}{2}$∠ABO-∠EFB=∠BOE-5°,
∵∠AEO=2∠OEF=2∠BOE=10°,
∴∠AEO=∠ABO+∠BAE+∠BOE=30°+∠BAE+∠EOB,
∴∠EOB-∠BAE=40°.
点评 本题考查了三角形的内角和,坐标与图形的关系,三角形的外角的性质,平行线的性质,熟练掌握各性质是解题的关键.

练习册系列答案
相关题目
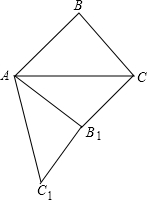 如图,在△ABC中,∠ABC=90°,AB=5,BC=4,将△ABC绕顶点A旋转到△AB1C1的位置(其中点B1对应点B,点C1对应点C),使得B1C∥AB,那么B1C=2.
如图,在△ABC中,∠ABC=90°,AB=5,BC=4,将△ABC绕顶点A旋转到△AB1C1的位置(其中点B1对应点B,点C1对应点C),使得B1C∥AB,那么B1C=2. 如图,∠B=∠E=90°,AC=DF,BF=EC,则除条件以外,相等的线段还有AB=DE,BC=EF,BF=CE..
如图,∠B=∠E=90°,AC=DF,BF=EC,则除条件以外,相等的线段还有AB=DE,BC=EF,BF=CE..