题目内容
6.设x1,x2是方程x2-x-2014=0的两实数根,则x13+2015x2-2013=2016.分析 先根据一元二次方程的解的定义得到x12=x1+2014,再计算x13=x12+2014x1=2015x1+2014,则原式可化简为2015×(x1+x2)+1,然后利用根与系数的关系求解.
解答 解:∵x1是方程x2-x-2014=0的根,
∴x12=x1+2014,
∴x13=x12+2014x1=x1+2014+2014x1=2015x1+2014,
∴原式=2015x1+2014+2015x2-2013=2015(x1+x2)+1,
∵x1,x2是方程x2-x-2014=0的两实数根,
∴x1+x2=1,
∴原式=2016.
故答案为:2016.
点评 本题考查了根与系数的关系,一元二次方程的解的定义,根据已知将原式化简,利用根与系数的关系是解答此题的关键.

练习册系列答案
相关题目
18.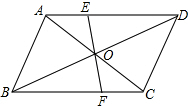 如图,已知平行四边形ABCD的两条对角线相交于点O,过点O的直线与AD,BC分别相交于E,F,则下列结论不正确的是( )
如图,已知平行四边形ABCD的两条对角线相交于点O,过点O的直线与AD,BC分别相交于E,F,则下列结论不正确的是( )
 如图,已知平行四边形ABCD的两条对角线相交于点O,过点O的直线与AD,BC分别相交于E,F,则下列结论不正确的是( )
如图,已知平行四边形ABCD的两条对角线相交于点O,过点O的直线与AD,BC分别相交于E,F,则下列结论不正确的是( )| A. | OE=OF | B. | △DOE≌△BOF | C. | S△ABC=S△BCD | D. | EF=AC |
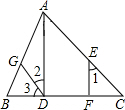 如图,已知AD⊥BC,EF⊥BC,∠3=∠C,求证:∠1=∠2.
如图,已知AD⊥BC,EF⊥BC,∠3=∠C,求证:∠1=∠2.
