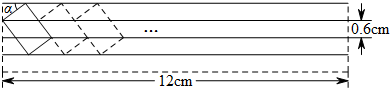
题目内容
6．已知，正n边形的一个内角为140°，则这个正n边形的边数是9．分析 根据多边形每个内角与其相邻的外角互补，则正n边形的每个外角的度数=180°-140°=40°，然后根据多边形的外角和为360°即可得到n的值．
解答 解：∵正n边形的每个内角都是140°，
∴正n边形的每个外角的度数=180°-140°=40°，
∴n=360÷40=9．
故答案为：9．
点评 本题考查了多边形内角与外角的关系及多边形的外角和定理，用到的知识点：
多边形每个内角与其相邻的外角互补；多边形的外角和为360°．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
如图，对?ABCD对角线交点O的直线分别交AB的延长线于点E，交CD的延长线于点F，若AB=4，AE=6，则DF的长等于2．
17．
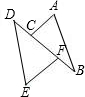如图，AB∥ED，CD=BF，若△ABC≌△EDF，则还需要补充的条件可以是（ ）
如图，AB∥ED，CD=BF，若△ABC≌△EDF，则还需要补充的条件可以是（ ）| A． | AC=EF | B． | BC=DF | C． | AB=DE | D． | ∠B=∠E |
将直尺和直角三角板按如图方式摆放，已知∠1=30°，则∠2的大小是60°．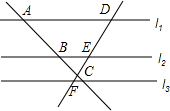
如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点A、B、C和D、E、F，已知$\frac{AB}{BC}$=$\frac{2}{3}$，则$\frac{DE}{DF}$=$\frac{2}{5}$．
