题目内容
 如图,已知EF⊥FD,AB⊥FD,CD⊥FD,EF=1.5,AB=2.5,FB=2.2,BD=3.6,求CD的长.
如图,已知EF⊥FD,AB⊥FD,CD⊥FD,EF=1.5,AB=2.5,FB=2.2,BD=3.6,求CD的长.考点:相似三角形的判定与性质
专题:
分析:如图,作辅助线,证明△EAG∽△ECH,列出比例式求出CH的长度即可解决问题.
解答: 解:如图,过点E作EH⊥DC,交AB于点G;
解:如图,过点E作EH⊥DC,交AB于点G;
∵EF⊥FD,AB⊥FD,CD⊥FD,
∴四边形EFBG,四边形GBDH均为矩形,
∴EG=FB=2.2,GH=BD=3.6,BG=HD=EF=1.5,
∴AG=2.5-1.5=1;
∵AG∥CH,
∴△EAG∽△ECH,
∴
=
,而EG=2.2,EH=5.8,AG=1,
∴CH=
,CD=
+
=
.
 解:如图,过点E作EH⊥DC,交AB于点G;
解:如图,过点E作EH⊥DC,交AB于点G;∵EF⊥FD,AB⊥FD,CD⊥FD,
∴四边形EFBG,四边形GBDH均为矩形,
∴EG=FB=2.2,GH=BD=3.6,BG=HD=EF=1.5,
∴AG=2.5-1.5=1;
∵AG∥CH,
∴△EAG∽△ECH,
∴
| AG |
| CH |
| EG |
| EH |
∴CH=
| 29 |
| 11 |
| 3 |
| 2 |
| 29 |
| 11 |
| 91 |
| 22 |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,已知:BD=DC,求证:EA•FB=EC•FA.
如图所示,已知:BD=DC,求证:EA•FB=EC•FA.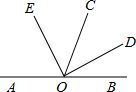 如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.