题目内容
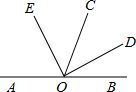 如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.(1)指出图中∠AOD的补角,∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)EO与DO具有怎样的位置关系?请说明理由.
考点:余角和补角
专题:
分析:(1)根据两个角的和是180°,这两个角互补;
(2)根据角平分线的性质,可得∠BOD=∠COD,∠EOC═∠AOC,可得答案;
(3)根据垂线的定义,可得答案.
(2)根据角平分线的性质,可得∠BOD=∠COD,∠EOC═∠AOC,可得答案;
(3)根据垂线的定义,可得答案.
解答:解:如图: ,
,
(1)由图形,得∠AOD的补角是∠BOD,∠BOE的补角是∠AOE;
(2)由OD平分∠BOC,得∠BOD=∠COD=
∠BOC=
×68°=34°;
由补角的性质,得∠AOC=180°-∠BOC=180°-68°=112°,
由OE平分∠AOC,得∠EOC═∠AOC=
∠112°=56°;
(3)EO⊥DO,理由如下:
由角的和差,得∠EOD=∠COD+∠COE=34°+56°=90°,
∴EO⊥DO.
 ,
,(1)由图形,得∠AOD的补角是∠BOD,∠BOE的补角是∠AOE;
(2)由OD平分∠BOC,得∠BOD=∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
由补角的性质,得∠AOC=180°-∠BOC=180°-68°=112°,
由OE平分∠AOC,得∠EOC═∠AOC=
| 1 |
| 2 |
(3)EO⊥DO,理由如下:
由角的和差,得∠EOD=∠COD+∠COE=34°+56°=90°,
∴EO⊥DO.
点评:本题考查了余角和补角,利用了补角的性质,角平分线的性质,垂线的定义.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
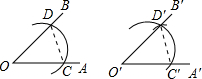 用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB依据是( )
用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB依据是( )| A、边边边 | B、边角边 |
| C、角边角 | D、角角边 |

 如图,已知EF⊥FD,AB⊥FD,CD⊥FD,EF=1.5,AB=2.5,FB=2.2,BD=3.6,求CD的长.
如图,已知EF⊥FD,AB⊥FD,CD⊥FD,EF=1.5,AB=2.5,FB=2.2,BD=3.6,求CD的长.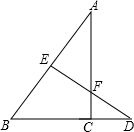 已知,CA⊥DB,DE⊥AB,AC、ED交于F,BC=3,FC=1,BD=5,则AC=
已知,CA⊥DB,DE⊥AB,AC、ED交于F,BC=3,FC=1,BD=5,则AC=