Question

17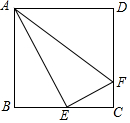．如图所示，在正方形ABCD中，E是BC的中点，F是CD上的一点，AE⊥EF，下列结论：①∠BAE=30°；②CE²=AB•CF；③CF=$\frac{1}{3}$FD；④△ABE∽△AEF，其中正确的有（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 设正方形的边长为2a，则BE=CE=a，AE=$\sqrt{5}$a，根据正切的定义可对①进行判断；通过证明Rt△ABE∽Rt△ECF，利用相似比得到CE²=AB•CF，则可对②进行判断；由②得到CF=$\frac{1}{2}$a，则DF=$\frac{3}{2}$a，于是可对③进行判断；利用勾股定理可得到EF=$\frac{\sqrt{5}}{2}$a，则有$\frac{AB}{AE}$=$\frac{BE}{EF}$，根据相似三角形的判定可得△ABE∽△AEF，则可对④进行判断．

解答 解：设正方形的边长为2a，则BE=CE=a，AE=$\sqrt{5}$a，
∵tan∠BAE=$\frac{BE}{AB}$=$\frac{1}{2}$，
∴∠BAE≠30°，所以①错误；
∵AE⊥EF，
∴∠AEB+∠FEC=90°，
而∠AEB+∠EAB=90°，
∴∠EAB=∠FEC，
∴Rt△ABE∽Rt△ECF，
∴$\frac{BE}{CF}$=$\frac{AB}{CE}$，
∴CE²=AB•CF，所以②正确；
即CF=$\frac{{a}^{2}}{2a}$=$\frac{1}{2}$a，
∴DF=CD-CF=2a-$\frac{1}{2}$a=$\frac{3}{2}$a，
∴CF=$\frac{1}{3}$DF，所以③正确；
在Rt△CEF中，EF=$\sqrt{{a}^{2}+（\frac{1}{2}a）^{2}}$=$\frac{\sqrt{5}}{2}$a，
∵$\frac{AB}{AE}$=$\frac{2a}{\sqrt{5}a}$=$\frac{2}{\sqrt{5}}$，$\frac{BE}{EF}$=$\frac{a}{\frac{\sqrt{5}}{2}a}$=$\frac{2}{\sqrt{5}}$，
∴$\frac{AB}{AE}$=$\frac{BE}{EF}$，
而∠ABE=∠AEF，
∴△ABE∽△AEF，所以④正确．
故选C．

点评 本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似；有两组角对应相等的两个三角形相似．也考查了正方形的性质．