题目内容
13.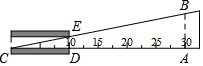 如图是测量玻璃管内径的示意图,点D正对“10mm”刻度线,点A正对“30mm”刻度线,DE∥AB.若量得AB的长为6mm,则内径DE的长为2mm.
如图是测量玻璃管内径的示意图,点D正对“10mm”刻度线,点A正对“30mm”刻度线,DE∥AB.若量得AB的长为6mm,则内径DE的长为2mm.
分析 直接利用相似三角形的判定与性质得出△CDE∽△CAB进而得出比例式求出答案.
解答 解:由题意可得:∵DE∥AB,
∴△CDE∽△CAB,
∴$\frac{DE}{AB}$=$\frac{DC}{AC}$,
即$\frac{DE}{6}$=$\frac{10}{30}$,
解得:DE=2,
故答案为:2.
点评 此题主要考查了相似三角形的应用,根据题意得出正确比例关系是解题关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
8.已知一个正数的两个平方根分别为2a-5和1-a,则这个正数为( )
| A. | 3 | B. | 4 | C. | 9 | D. | 16 |
5.由于微电子技术的不断进步,可以在300平方毫米的芯片上集成6亿个元件,平均每个元件约占( )
| A. | 5×10-7毫米2 | B. | 5×10-8毫米2 | C. | 2×106毫米2 | D. | 2×107毫米2 |
2.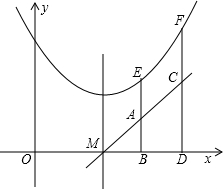 如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
 如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )| A. | S=y2+y1 | B. | S=y2+2y1 | C. | S=y2-y1 | D. | S=y2-2y1 |
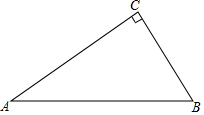 如图.△ABC是直角三角形,∠ACB=90°,∠A=30°.
如图.△ABC是直角三角形,∠ACB=90°,∠A=30°.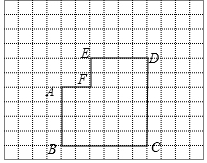 下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.