题目内容
1.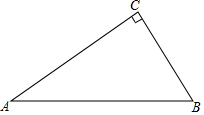 如图.△ABC是直角三角形,∠ACB=90°,∠A=30°.
如图.△ABC是直角三角形,∠ACB=90°,∠A=30°.(1)实践与操作:利用尺规按下列要求作图.并在图中标明相应字母(保留作图痕迹.不写作法).
①作△ABC的外接圆O;
②在AB的延长线上作一点D,使得CD与⊙O相切;
(2)综合与运用:在你所作的图中.若AC=6,则由线段CD、BD及$\widehat{BC}$所围成图形的面积为6$\sqrt{3}$-2π.
分析 (1)①作线段AB的垂直平分线EF交AB于O,以O为圆心OA为半径作⊙O,⊙O即为所求;②过点C作OC的垂线,交AB的延长线于D,直线CD即为所求;
(2)先求得OC,CD以及∠COB的度数,再根据CD,BD及$\widehat{BC}$所围成图形的面积=S△DOC-S扇形O-BC计算即可;
解答 解:(1)①作线段AB的垂直平分线EF交AB于O,以O为圆心OA为半径作⊙O,则⊙O即为所求.
②过点C作OC的垂线,交AB的延长线于D,则点D即为所求.
(2)∵AC=6,∠A=30°,
∴BC=tan30°×6=2$\sqrt{3}$,∠COB=60°,
又∵OC=OB,
∴△COB是等边三角形,
∴OC=2$\sqrt{3}$,
∵CD与⊙O相切,
∴∠OCD=90°,
∴∠D=30°,
∴DO=2OC=4$\sqrt{3}$,
∴DC=6,
∴线段CD,BD及$\widehat{BC}$所围成图形的面积=S△DOC-S扇形OBC=$\frac{1}{2}$×2$\sqrt{3}$×6-$\frac{60π×(2\sqrt{3})^{2}}{360}$=6$\sqrt{3}$-2π.
故答案为:6$\sqrt{3}$-2π.
点评 本题考查作图-复杂作图、三角形的外接圆与外心、切线的判定和性质等知识,解题的关键是熟练掌握基本作图,学会用分割法求图形面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图所示是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( )
如图所示是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( )
 如图所示是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( )
如图所示是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( )| A. | 40×70×80 | B. | 80×80×40 | C. | 40×40×70 | D. | 70×70×80 |
10.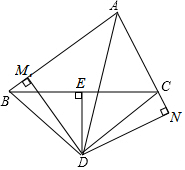 如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC的延长线于点N,下列结论中错误的是( )
如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC的延长线于点N,下列结论中错误的是( )
 如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC的延长线于点N,下列结论中错误的是( )
如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC的延长线于点N,下列结论中错误的是( )| A. | DM=DN | B. | ∠ABD+∠ACD=180° | ||
| C. | AC+AN=AB | D. | BC2+4DE2=4BM2+4DM2 |
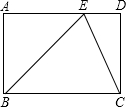 如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=5.
如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=5.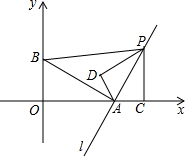 如图,在直角坐标系中,点A(2,0),点B(0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处.若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为P(5,2),p(8,8),P(0,-8),P(3,-2).
如图,在直角坐标系中,点A(2,0),点B(0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处.若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为P(5,2),p(8,8),P(0,-8),P(3,-2).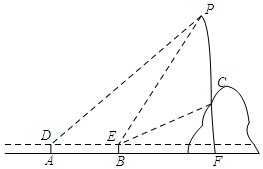 如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.
如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.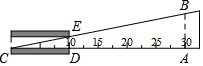 如图是测量玻璃管内径的示意图,点D正对“10mm”刻度线,点A正对“30mm”刻度线,DE∥AB.若量得AB的长为6mm,则内径DE的长为2mm.
如图是测量玻璃管内径的示意图,点D正对“10mm”刻度线,点A正对“30mm”刻度线,DE∥AB.若量得AB的长为6mm,则内径DE的长为2mm.