题目内容
11.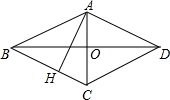 如图,在平行四边形ABCD中,对角线AC与BD相交于O,AC=2,BD=4.AB=$\sqrt{5}$,则平行四边形ABCD的高AH的长为$\frac{4\sqrt{5}}{5}$.
如图,在平行四边形ABCD中,对角线AC与BD相交于O,AC=2,BD=4.AB=$\sqrt{5}$,则平行四边形ABCD的高AH的长为$\frac{4\sqrt{5}}{5}$.
分析 先由平行四边形的性质得出OA=1,OB=2,再根据勾股定理的逆定理得出∠AOB=90°,那么平行四边形ABCD是菱形,然后根据菱形的面积不变求出AH的长.
解答 解:∵在平行四边形ABCD中,对角线AC与BD相交于O,AC=2,BD=4,
∴OA=$\frac{1}{2}$AC=1,OB=$\frac{1}{2}$=2,
∴OA2+OB2=1+4=5=AB2,
∴△AOB是直角三角形,∠AOB=90°,
∴平行四边形ABCD是菱形,
∴BC=AB=$\sqrt{5}$,
∴S菱形ABCD=BC•AH=$\frac{1}{2}$AC•BD,
∴AH=$\frac{\frac{1}{2}×2×4}{\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$.
故答案为$\frac{4\sqrt{5}}{5}$.
点评 此题主要考查了平行四边形的性质,菱形的判定与性质,勾股定理的逆定理,关键是根据勾股定理的逆定理得出∠AOB=90°,再利用菱形的面积公式列式计算.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
16.点A(-5,y1)和B(-2,y2)都在直线y=kx(k<0)上,则y1与y2的关系是( )
| A. | y1≤y2 | B. | y1=y2 | C. | y1>y2 | D. | y1<y2 |
20.已知点平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )
| A. | -3 | B. | -5 | C. | 1或-3 | D. | 1或-5 |
 如图,B处在A处的南偏西60°方向,C处在A处的南偏东20°方向,C处在B处的正东方向,求∠ACB的度数.
如图,B处在A处的南偏西60°方向,C处在A处的南偏东20°方向,C处在B处的正东方向,求∠ACB的度数. 到直线l1、l2的距离相等的点的轨迹是什么?
到直线l1、l2的距离相等的点的轨迹是什么?
 已知一次函数y=-2x+2
已知一次函数y=-2x+2