题目内容
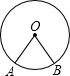如图，A、B是⊙O上两点，且∠AOB=70°，点C是⊙O上不与点A、B重合的任一点，则∠ACB的度数是（ ）| A、35° |
| B、145° |
| C、35°或145° |
| D、35°或110° |
考点：圆周角定理
专题：
分析：分别从当点C在优弧AB上时与当点C在劣弧AB上时去分析，利用圆周角定理与圆的内接四边形的性质，即可求得答案．
解答：解：∵当点C在优弧AB上时，∠ACB=
∠AOB=
×70°=35°；
当点C在劣弧AB上时，∠ACB=180°-35°=145°．
∴∠ACB的度数是35°或145°．
故选C．
| 1 |
| 2 |
| 1 |
| 2 |
当点C在劣弧AB上时，∠ACB=180°-35°=145°．
∴∠ACB的度数是35°或145°．
故选C．
点评：此题考查了圆周角定理以及圆的内接四边形的性质．此题难度不大，注意掌握数形结合思想与分类讨论思想的应用．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
三角形的两边分别2和6，第三边是方程x2-10x+21=0的解，则三角形周长为（ ）
| A、11 | B、15 |
| C、11或15 | D、不能确定 |
下列计算中错误的是（ ）
A、a
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
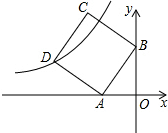如图，在平面直角坐标系中，直线y=2x+4与x轴、y轴分别交于A、B两点，以AB为边在第二象限作正方形ABCD，点D在双曲线y=
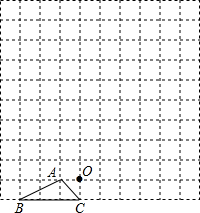图中的小方格都是边长为1的正方形，△ABC的顶点和O点都在正方形的顶点上．以点O为位似中心，在方格图中将△ABC放大为原来的2倍，得到△A′B′C′，再将△A′B′C′绕点B′顺时针旋转90°，旋转后得到△A″B′C″，请将△A′B′C′和△A″B′C″在正方形中分别画出，并保留作图痕迹．
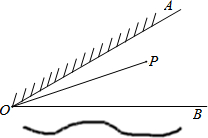如图，∠AOB=30°，OA表示草地边，OB表示河边，点P表示家且在∠AOB内．某人要从家里出发先到草地边给马喂草，然后到河边喂水，最后回到家里．