题目内容
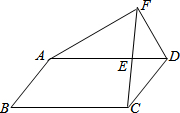 如图,已知点E在平行四边形ABCD的边AD上,AE=3ED,延长CE到点F,使得EF=CE,设
如图,已知点E在平行四边形ABCD的边AD上,AE=3ED,延长CE到点F,使得EF=CE,设| BA |
| a |
| BC |
| b |
| a |
| b |
| CE |
| AF |
考点:*平面向量
专题:
分析:由四边形ABCD是平行四边形,可得
=
=
,
=
=
,又由AE=3ED,即可求得
与
的长,然后由三角形法则,求得向量
和
.
| CD |
| BA |
| a |
| AD |
| BC |
| b |
| AE |
| ED |
| CE |
| AF |
解答:解:∵四边形ABCD是平行四边形,
∴
=
=
,
=
=
,
∵AE=3ED,
∴
=
=
,
=
=
,
∴
=
-
=
-
;
∵EF=CE,
∴
=
=
-
,
∴
=
+
=
+
-
=
+
.
∴
| CD |
| BA |
| a |
| AD |
| BC |
| b |
∵AE=3ED,
∴
| AE |
| 3 |
| 4 |
| AD |
| 3 |
| 4 |
| b |
| ED |
| 1 |
| 4 |
| AD |
| 1 |
| 4 |
| b |
∴
| CE |
| CD |
| ED |
| a |
| 1 |
| 4 |
| b |
∵EF=CE,
∴
| EF |
| CE |
| a |
| 1 |
| 4 |
| b |
∴
| AF |
| AE |
| EF |
| 3 |
| 4 |
| b |
| a |
| 1 |
| 4 |
| b |
| a |
| 1 |
| 2 |
| b |
点评:此题考查了平面向量的知识.此题难度适中,注意掌握三角形法则的应用,注意掌握数形结合思想的应用.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
如果□+2=0,那么“□”内应填的实数是( )
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
若关于x的二次函数y=kx2+2x-1的图象与x轴仅有一个公共点,则k的取值范围是( )
| A、k=0 | B、k=-1 |
| C、k>-1 | D、k≠0且k=-1 |
⊙O的半径为5cm,弦AB∥CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
| A、1cm |
| B、7cm |
| C、3cm或4cm |
| D、1cm或7cm |
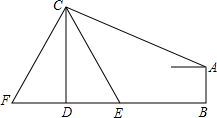 如图,在电线杆上的C处引拉线CE、CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处得仰角为23°,已知测角仪AB的高为1.5米,求拉线CE的长.
如图,在电线杆上的C处引拉线CE、CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处得仰角为23°,已知测角仪AB的高为1.5米,求拉线CE的长.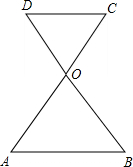 如图,AC与BD相交于点O,若OA=OB,∠A=60°,且AB∥CD,求证:△OCD是等边三角形.
如图,AC与BD相交于点O,若OA=OB,∠A=60°,且AB∥CD,求证:△OCD是等边三角形.