题目内容
解方程:
(1)x2-6x-6=0;
(2)
-
=1.
(1)x2-6x-6=0;
(2)
| 6 |
| x2-1 |
| 3 |
| x-1 |
考点:解一元二次方程-公式法,解分式方程
专题:
分析:(1)先求出b2-4ac的值,再代入公式求出即可;
(2)先把分式方程转化成整式方程,求出整式方程的解,最后进行检验即可.
(2)先把分式方程转化成整式方程,求出整式方程的解,最后进行检验即可.
解答:解:(1)x2-6x-6=0,
b2-4ac=(-6)2-4×1×(-6)=60,
x=
,
x1=3+
,x2=3-
;
(2)方程两边都乘以(x+1)9x-1)得:6-3(x+1)=(x+1)(x-1),
即x2+3x-4=0,
解得:x1=1,x2=-4,
经检验x=1为增根,x=4是原方程的根,
即原方程的解为x=4.
b2-4ac=(-6)2-4×1×(-6)=60,
x=
6±
| ||
| 2 |
x1=3+
| 15 |
| 15 |
(2)方程两边都乘以(x+1)9x-1)得:6-3(x+1)=(x+1)(x-1),
即x2+3x-4=0,
解得:x1=1,x2=-4,
经检验x=1为增根,x=4是原方程的根,
即原方程的解为x=4.
点评:本题考查了解一元二次方程和解分式方程的应用,主要考查学生的计算能力,注意:解分式方程一定要进行检验.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
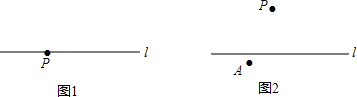 我们知道“经过一点有且只有一条直线与已知直线垂直”,那么如何用(不带刻度)直尺和圆规来作图呢?
我们知道“经过一点有且只有一条直线与已知直线垂直”,那么如何用(不带刻度)直尺和圆规来作图呢? 如图,边长为4的菱形ABCD的内角∠B=60°,O是对角线AC的中点.E、F、G、H 分别在菱形ABCD的四条边上,四边形EBOF与四边形HDOG关于直线AC对称,且∠EOF=60°.
如图,边长为4的菱形ABCD的内角∠B=60°,O是对角线AC的中点.E、F、G、H 分别在菱形ABCD的四条边上,四边形EBOF与四边形HDOG关于直线AC对称,且∠EOF=60°.