题目内容
 如图所示,AB⊥BC,AD∥BC,以AB为直径的⊙O与CD相切于G点,且DO=6,CO=8,求⊙O的直径AB.
如图所示,AB⊥BC,AD∥BC,以AB为直径的⊙O与CD相切于G点,且DO=6,CO=8,求⊙O的直径AB.考点:切线的性质
专题:
分析:由AD∥BC,AB⊥BC就可以得出∠A=∠B=90°,由AB是直径就可以得出AD、BC是⊙O的切线,由切线长定理就可以得出∠AOD=∠GOD,∠COG=∠COB,由平角的定义就可以得出∠COD=90°,由勾股定理就可以求出CD的值,再由三角形的面积公式就可以求出OG的值,进而得出结论.
解答:解:∵AB⊥BC,
∴∠B=90°.
∵AD∥BC,
∴∠A+∠B=180°,
∴∠A=∠B=90°.
∵⊙O与CD相切于G点,
∴OG⊥CD.∠AOD=∠GOD,∠COG=∠COB.
∵∠AOD+∠GOD+∠COG+∠COB=180°,
∴∠GOD+∠GOD+∠COG+∠COG=180°,
∴∠GOD+∠COG=90°.
即∠COD=90°,
∴CD2=OD2+OC2.
∵DO=6,CO=8,
∴CD=10.
∵
=
,
∴
=
,
∴OG=
.
∴⊙O的直径AB=
.
答:⊙O的直径AB=
.
∴∠B=90°.
∵AD∥BC,
∴∠A+∠B=180°,
∴∠A=∠B=90°.
∵⊙O与CD相切于G点,
∴OG⊥CD.∠AOD=∠GOD,∠COG=∠COB.
∵∠AOD+∠GOD+∠COG+∠COB=180°,
∴∠GOD+∠GOD+∠COG+∠COG=180°,
∴∠GOD+∠COG=90°.
即∠COD=90°,
∴CD2=OD2+OC2.
∵DO=6,CO=8,
∴CD=10.
∵
| OD•OC |
| 2 |
| CD•OG |
| 2 |
∴
| 6×8 |
| 2 |
| 10OG |
| 2 |
∴OG=
| 24 |
| 5 |
∴⊙O的直径AB=
| 48 |
| 5 |
答:⊙O的直径AB=
| 48 |
| 5 |
点评:本题考查了平行线的性质的运用,垂直的性质的运用,切线长定理的运用,勾股定理的运用,切线的性质的运用,三角形的面积公式的运用,解答时运用切线的性质求解是关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )| A、40° | B、45° |
| C、50° | D、55° |
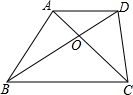 如图所示,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD:BC=2:3,求S△AOD:S△BOA.
如图所示,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD:BC=2:3,求S△AOD:S△BOA. 如图,有点A、B、C、D,请画出一点P,使PA=PB,PC=PD.
如图,有点A、B、C、D,请画出一点P,使PA=PB,PC=PD.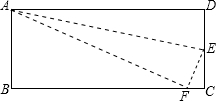 如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,求DE的长.
如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,求DE的长. 如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与x轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD?若存在,求出P点坐标.
如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与x轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD?若存在,求出P点坐标.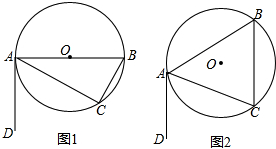 如图1,⊙O中,AB为直径,AC为弦,过A作直线DA,使∠DAC=∠B.
如图1,⊙O中,AB为直径,AC为弦,过A作直线DA,使∠DAC=∠B.