题目内容
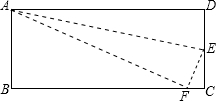 如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,求DE的长.
如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,求DE的长.考点:翻折变换(折叠问题)
专题:
分析:根据三角形的面积求出BF,利用勾股定理列式求出AF,再根据翻折变换的性质可得AD=AF,然后求出CF,设DE=x,表示出EF、EC,然后在Rt△CEF中,利用勾股定理列方程求解即可.
解答:解:在长方形ABCD中,DC=5cm,
所以,AB=DC=5cm,
∵△ABF的面积为30cm2,
∴
×5•BF=30,
解得BF=12cm,
由勾股定理得,AF=
=
=13cm,
∵△AED沿AE折叠点D落在BC上点F处,
∴AD=AF=13cm,DE=EF,
∴CF=BC-BF=13-12=1cm,
设DE=x,则EF=x,EC=5-x,
在Rt△CEF中,由勾股定理得,CF2+EC2=EF2,
即12+(5-x)2=x2,
解得x=2.6,
所以DE=2.6cm.
所以,AB=DC=5cm,
∵△ABF的面积为30cm2,
∴
| 1 |
| 2 |
解得BF=12cm,
由勾股定理得,AF=
| AB2+BF2 |
| 52+122 |
∵△AED沿AE折叠点D落在BC上点F处,
∴AD=AF=13cm,DE=EF,
∴CF=BC-BF=13-12=1cm,
设DE=x,则EF=x,EC=5-x,
在Rt△CEF中,由勾股定理得,CF2+EC2=EF2,
即12+(5-x)2=x2,
解得x=2.6,
所以DE=2.6cm.
点评:本题考查了翻折变换的性质,矩形的性质,三角形的面积,勾股定理,熟记各性质并利用勾股定理列出方程是解题的关键.

练习册系列答案
相关题目
绝对值为5的数是( )
| A、5 | B、-5 |
| C、5或-5 | D、0或5 |
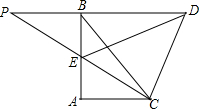 如图,AB⊥AC,AB=AC=2,过点B作直线l⊥AB,点P是直线l上点B左侧的一个动点,联结PC交AB于点E,过点C作CD⊥PC交直线l于点D.
如图,AB⊥AC,AB=AC=2,过点B作直线l⊥AB,点P是直线l上点B左侧的一个动点,联结PC交AB于点E,过点C作CD⊥PC交直线l于点D. 尺规作△ABC的外接圆.(请保留作图痕迹)
尺规作△ABC的外接圆.(请保留作图痕迹) 如图所示,AB⊥BC,AD∥BC,以AB为直径的⊙O与CD相切于G点,且DO=6,CO=8,求⊙O的直径AB.
如图所示,AB⊥BC,AD∥BC,以AB为直径的⊙O与CD相切于G点,且DO=6,CO=8,求⊙O的直径AB.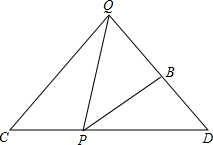 已知QC=QD=2,∠C=∠D=∠QPB=45°,P在CD上运动不与C、D重合,设CP=x,QB=y,求y关于x的函数关系式.
已知QC=QD=2,∠C=∠D=∠QPB=45°,P在CD上运动不与C、D重合,设CP=x,QB=y,求y关于x的函数关系式.