Question

如图，抛物线y=-x²+2x+3与x轴分别交于A、B两点，与x轴的正半轴交于C点，抛物线的顶点为D，连接BC、BD，抛物线上是否存在一点P，使得∠PCB=∠CBD？若存在，求出P点坐标．

Answer 1

考点：抛物线与x轴的交点

专题：

分析：根据题意得出A，B，C的坐标，进而得出△BCD是直角三角形，再过B点作BE垂直于BC，连接EC，且BE=

2

，求出△ECB≌△DBC（SAS），进而得出EC直线解析式，即可得出P点坐标．

解答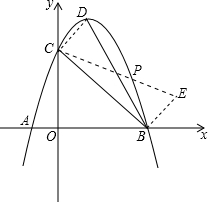：解：连接DC，
当y=0则0=-x²+2x+3，
解得：x₁=-1，x₂=3，
当x=0，则y=3，
故A（-1 0），B（3 0），C（0 3），
y=-x²+2x+3
=-（x-1）²+4，
故D（1 4），
因此BC=

32+32

=

18

=3

2

，
BD=

42+22

=2

5

，CD=

12+12

=

2

，
故CD²+BD²=BC²，
因此满足△BCD是直角三角形且∠BCD=90°，
过B点作BE垂直于BC，连接EC，且BE=

2

，
∵CO=OB=3，
∴∠OCB=∠CBO=45°，
故∠EBx=45°，
则E（4 1），
在△ECB和△DBC中，

BE=CD ∠DCB=∠CBE BE=CB

，
∴△ECB≌△DBC（SAS），
此时CE与抛物线的交点就是满足条件的点P，
设直线EC的解析式为：y=kx+b，
则

b=3 4k+b=1

，
解得：

k=-0.5 b=3

．
则EC直线解析式为：y=-0.5x+3，
故-0.5x+3=-x²+2x+3，
解得：x₁=0（不合题意舍去），x₂=2.5，
则y=1.75，
故P点坐标为：（2.5 1.75）．

点评：此题主要考查了抛物线与坐标轴的交点以及全等三角形的判定与性质和抛物线与一次函数的交点求法等知识，求出EC解析式是解题关键．