题目内容
3.已知一元二次方程x2-2x+m=0的两实数根为x1和x2,且x1+3x2=5,则m的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | -$\frac{3}{4}$ |
分析 首先根据根与系数的关系得出x1+x2=2,与x1+3x2=3,组成方程组求得x1,x2,进一步得出x1x2=m求得答案即可.
解答 解:∵一元二次方程x2-2x+m=0的两根为x1,x2,
∴x1+x2=2,
则$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2}\\{{x}_{1}+3{x}_{2}=5}\end{array}\right.$
解得x1=$\frac{1}{2}$,x2=$\frac{3}{2}$
∴m=x1x2=$\frac{3}{4}$.
点评 本题考查了根与系数的关系.二次项系数为1,常用以下关系:x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q,反过来可得p=-(x1+x2),q=x1x2,前者是已知系数确定根的相关问题,后者是已知两根确定方程中未知系数.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
13.方程组$\left\{\begin{array}{l}{x+y=10}\\{2x+y=16}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=6}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=8}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=9}\\{y=-1}\end{array}\right.$ |
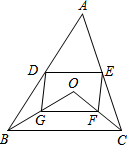 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.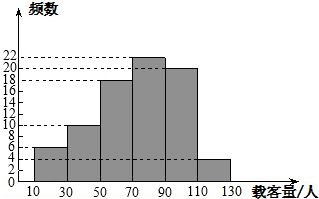 为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.(注:一个小组的组中值是指这个小组的两个端点数的平均数)
为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.(注:一个小组的组中值是指这个小组的两个端点数的平均数) 如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2015,最少经过( )次操作.
如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2015,最少经过( )次操作.