题目内容
14.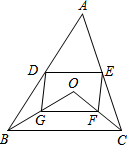 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.(1)求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)
分析 (1)首先利用三角形中位线的性质得出DE∥BC,DE=$\frac{1}{2}$BC,同理,GF∥BC,GF=$\frac{1}{2}$BC,即可得出DE∥GF,DE=GF即可得出四边形DGFE是平行四边形;
(2)OA=BC时四边形DGFE是菱形,利用(1)中所求,只要邻边再相等即可得出答案.
解答 (1)证明:∵D、E分别是边AB、AC的中点.
∴DE∥BC,DE=$\frac{1}{2}$BC.
同理,GF∥BC,GF=$\frac{1}{2}$BC.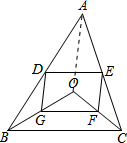
∴DE∥GF,DE=GF.
∴四边形DEFG是平行四边形;
(2)OA=BC时四边形DGFE是菱形,
理由如下:
连接OA.由(1)得出四边形DEFG是平行四边形,
∴AO=BC,
∴GD=$\frac{1}{2}$AO,GF=$\frac{1}{2}$BC,
∴DG=GE,
∴平行四边形DEFG是菱形.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,菱形的判定以及平行四边形与菱形的关系,熟记的定理和性质是解题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
6.下列不等式中,解集是x>1的不等式是( )
| A. | 3x>-3 | B. | x+4≥3 | C. | 2x+3>5 | D. | -2x+3<5 |
3.已知一元二次方程x2-2x+m=0的两实数根为x1和x2,且x1+3x2=5,则m的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | -$\frac{3}{4}$ |
 如图,AD、AE分别是△ABC的高和角平分线,∠C=36°,∠B=72°,则∠DAE的度数为18°(度).
如图,AD、AE分别是△ABC的高和角平分线,∠C=36°,∠B=72°,则∠DAE的度数为18°(度).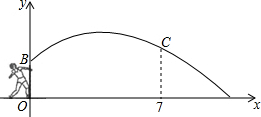 如图是医学生投掷铅球时,铅球运行的高度y(m)与水平距离x(m)的函数图象,其解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$.
如图是医学生投掷铅球时,铅球运行的高度y(m)与水平距离x(m)的函数图象,其解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$. 如图,从点A(0,2)出发的一束光,经x轴反射,过点B(3,4),则入射点C的坐标是(1,0).
如图,从点A(0,2)出发的一束光,经x轴反射,过点B(3,4),则入射点C的坐标是(1,0).