题目内容
18.在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一直线上,当△ABC的周长最小时,点C的坐标可能是( )| A. | (0,0) | B. | (0,-1) | C. | (0,5) | D. | (0,3) |
分析 根据轴对称作最短路线得出AE=B′E,进而得出B′O=C′O,即可得出△ABC的周长最小时C点坐标.
解答 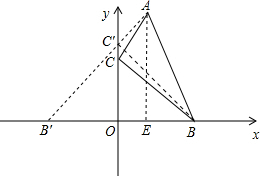 解:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,
解:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,
此时△ABC的周长最小,
∵点A、B的坐标分别为(1,4)和(3,0),
∴B′点坐标为:(-3,0),AE=4,
则B′E=4,即B′E=AE,
∵C′O∥AE,
∴B′O=C′O=3,
∴点C′的坐标是(0,3).
故选D.
点评 此题主要考查了利用轴对称求最短路线以及平行线的性质和勾股定理的运用,根据已知得出C点位置是解题关键.

练习册系列答案
相关题目
3.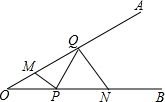 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )
 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )| A. | ∠1+∠2=90° | B. | 2∠2-∠1=30° | C. | 2∠1+∠2=180° | D. | ∠1-∠2=90° |
10.某厂一周计划生产700个零件,平均每天生产100个,由于各种原因实际每天生产量与计划量相比有出入,如表是某周每天的生产情况(超产为正,减产为负.单位:个)
该厂实行计件工资制,每生产一个零件10元,若当天超额完成任务,当天超出部分每个15元,若当天完不成任务当天生产出的零件每个只能按5元发工资,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +2 | -3 | -1 | +8 | -7 | +10 | -5 |
 如图,△ABC中,DE是AC的垂直平分线,△BCD和△ABC的周长分别为14和22,则AE长为4.
如图,△ABC中,DE是AC的垂直平分线,△BCD和△ABC的周长分别为14和22,则AE长为4.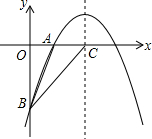 如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象经过A (2,0),B(0,-6)两点.求这个二次函数的解析式.
如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象经过A (2,0),B(0,-6)两点.求这个二次函数的解析式. 如图,在l上找一点P,使|PA-PB|最大.
如图,在l上找一点P,使|PA-PB|最大.