题目内容
8.已知关于x的一元二次方程x2+2x-a=0有两个不相等的实数根.(1)试确定a的取值范围;
(2)若a的最小值为b,且x=1-$\sqrt{3}$-b,求代数式(7+4$\sqrt{3}$)x2+(2+$\sqrt{3}$)x+$\sqrt{3}$的值.
分析 (1)由方程有两个不相等的实数根可得出△>0,套入数据即可得出关于a的一元一次不等式,解不等式即可得出结论;
(2)结合(1)的结论确定b的值,将其带入x=1-$\sqrt{3}$-b中得出x的值,再将x的值带入到代数式中利用整式运算的运算法则即可得出结论.
解答 解:(1)由已知得:△=b2-4ac=22+4a>0,
解得:a>-1.
(2)∵a的最小值为b,
∴b=-1.
∴x=1-$\sqrt{3}$-b=1-$\sqrt{3}$-(-1)=2-$\sqrt{3}$,
∴(7+4$\sqrt{3}$)x2+(2+$\sqrt{3}$)x+$\sqrt{3}$,
=(7+4$\sqrt{3}$)(2-$\sqrt{3}$)2+(2+$\sqrt{3}$)(2-$\sqrt{3}$)+$\sqrt{3}$,
=49-48+4-3+$\sqrt{3}$,
=2+$\sqrt{3}$.
点评 本题考查了根的判别式、解一元一次不等式以及整式的运算,结题的关键是:(1)得出关于a的一元一次不等式;(2)得出x的值.本题属于基础题,难度不大,解决该题型题目时,根据根的个数利用根的判别式得出一元一次方程(或不等式)是关键.

练习册系列答案
相关题目
18.如图,是一组按照某种规律摆放而成的图案,则第5个图形中三角形的个数是( )

| A. | 17 | B. | 16 | C. | 9 | D. | 8 |
19. 如图,下列条件中,不能推断AB∥CD的是( )
如图,下列条件中,不能推断AB∥CD的是( )
 如图,下列条件中,不能推断AB∥CD的是( )
如图,下列条件中,不能推断AB∥CD的是( )| A. | ∠B=∠5 | B. | ∠1=∠2 | C. | ∠3=∠4 | D. | ∠B+∠BCD=180° |
20.化简$\root{3}{8}$的结果是( )
| A. | 8 | B. | 4 | C. | -2 | D. | 2 |
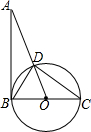 如图,AB=12,且AB为⊙O的切线,BC为⊙O的直径,AO与⊙O交于点D、AD=8.
如图,AB=12,且AB为⊙O的切线,BC为⊙O的直径,AO与⊙O交于点D、AD=8. 解不等式组$\left\{\begin{array}{l}{5+2x≥3}&{①}\\{\frac{x+1}{3}>\frac{x}{2}}&{②}\end{array}\right.$,并把该不等式组的解集表示在数轴上.
解不等式组$\left\{\begin{array}{l}{5+2x≥3}&{①}\\{\frac{x+1}{3}>\frac{x}{2}}&{②}\end{array}\right.$,并把该不等式组的解集表示在数轴上. 如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.