题目内容
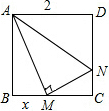正方形ABCD边长为2，M、N分别为BC、CD上的点，AM⊥MN，BM=x，求x为何值时，△ABM∽△AMN？考点：相似三角形的判定
专题：
分析：由相似三角形的对应边成比例，即可得当
=
时，△ABM∽△AMN，继而可求得答案．
| AB |
| BM |
| AM |
| MN |
解答：解：设BM=x，
∵正方形ABCD边长为2，
∴CM=BC-BM=2-x，
∵△ABM∽△MCN，
∴AB：CM=BM：CN，
∴
=
，
∴CN=
，
∴在Rt△ABM中，AM2=AB2+BM2=4+x2，
在Rt△CMN中，MN2=CM2+CN2=（2-x）2+[
]2=
，
∵∠B=∠AMN=90°，
∴当
=
时，△ABM∽△AMN，
∴当
=
，即
=
时，△ABM∽△AMN，
解得：x=1．
故当x=1时△ABM与△AMN相似．
∵正方形ABCD边长为2，
∴CM=BC-BM=2-x，
∵△ABM∽△MCN，
∴AB：CM=BM：CN，
∴
| 2 |
| 2-x |
| x |
| CN |
∴CN=
| x(2-x) |
| 2 |
∴在Rt△ABM中，AM2=AB2+BM2=4+x2，
在Rt△CMN中，MN2=CM2+CN2=（2-x）2+[
| x(2-x) |
| 2 |
| (2-x)2(x2+4) |
| 4 |
∵∠B=∠AMN=90°，
∴当
| AB |
| BM |
| AM |
| MN |
∴当
| AB2 |
| BM2 |
| AM2 |
| MN2 |
| 4 |
| x2 |
| 4+x2 | ||
|
解得：x=1．
故当x=1时△ABM与△AMN相似．
点评：此题考查了相似三角形的判定与性质、正方形的性质以及勾股定理等知识．此题难度较大，注意掌握数形结合思想与方程思想的应用．
练习册系列答案
相关题目
如图，在菱形ABCD中，AE⊥BC于点E，CE=1，且计算
-y的结果是（ ）
| 1 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|