题目内容
 如图,在菱形ABCD中,AE⊥BC于点E,CE=1,且
如图,在菱形ABCD中,AE⊥BC于点E,CE=1,且| AE |
| BC |
| 5 |
| 13 |
考点:菱形的性质
专题:
分析:设AE=5x,表示出BC=13x,再根据菱形的四条边都相等可得AB=13x,然后表示出BE,再利用勾股定理列方程求出AB,然后根据菱形的周长公式列式计算即可得解.
解答:解:∵
=
,
∴设AE=5x,则BC=13x,
在菱形ABCD中,AB=BC=13x,
∵CE=1,
∴BE=13x-1,
在Rt△ABE中,由勾股定理得,
AB2=BE2+AE2,
即(13x)2=(13x-1)2+(5x)2,
整理得,25x2-26x+1=0,
解得x1=1,x2=
(舍去),
∴BC=13,
菱形的周长=13×4=52.
| AE |
| BC |
| 5 |
| 13 |
∴设AE=5x,则BC=13x,
在菱形ABCD中,AB=BC=13x,
∵CE=1,
∴BE=13x-1,
在Rt△ABE中,由勾股定理得,
AB2=BE2+AE2,
即(13x)2=(13x-1)2+(5x)2,
整理得,25x2-26x+1=0,
解得x1=1,x2=
| 1 |
| 25 |
∴BC=13,
菱形的周长=13×4=52.
点评:本题考查了菱形的性质,勾股定理,锐角三角函数的定义,难点在于利用勾股定理列出方程.

练习册系列答案
相关题目
 如图,四个圆的半径都是1,顺次连接四个圆心得到四边形ABCD,则图中阴影部分的面积之和是
如图,四个圆的半径都是1,顺次连接四个圆心得到四边形ABCD,则图中阴影部分的面积之和是 如图,长方形ABCD中,AB=8cm,BC=15cm,E是BC的中点,F是CD的中点,BD、AE、AF把长方形分成了六块,阴影部分总面积是多少?
如图,长方形ABCD中,AB=8cm,BC=15cm,E是BC的中点,F是CD的中点,BD、AE、AF把长方形分成了六块,阴影部分总面积是多少?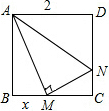 正方形ABCD边长为2,M、N分别为BC、CD上的点,AM⊥MN,BM=x,求x为何值时,△ABM∽△AMN?
正方形ABCD边长为2,M、N分别为BC、CD上的点,AM⊥MN,BM=x,求x为何值时,△ABM∽△AMN? 已知:如图,直线AB∥ED,求证:∠ABC+∠CDE=∠BCD.
已知:如图,直线AB∥ED,求证:∠ABC+∠CDE=∠BCD.