题目内容
 如图,在Rt△ABC中,AB=4,BC=3,在Rt△FAC中,AF=12,求正方形CDEF的面积.
如图,在Rt△ABC中,AB=4,BC=3,在Rt△FAC中,AF=12,求正方形CDEF的面积.考点:勾股定理
专题:
分析:利用勾股定理求出AC的平方,再利用勾股定理求出FC的平方即得正方形的面积.
解答:解:∵∠FAC和∠ABC都为直角,
∴AC2=AB2+BC2=25,FC2=FA2+AC2=144,
∴FC2=FA2+AC2=144+25=169.
∴正方形CDEF的面积为169.
∴AC2=AB2+BC2=25,FC2=FA2+AC2=144,
∴FC2=FA2+AC2=144+25=169.
∴正方形CDEF的面积为169.
点评:本题考查了勾股定理的运用,在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
相关题目
下面有4个图案,其中是轴对称图形的是( )


| A、②③④ | B、①②③ |
| C、①②④ | D、①②③④ |
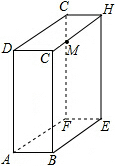 如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少? 如图,在正方形网格中,每个小正方形的边长都是1,△ABC的顶点均在格点上,试判断△ABC是否为直角三角形?为什么?
如图,在正方形网格中,每个小正方形的边长都是1,△ABC的顶点均在格点上,试判断△ABC是否为直角三角形?为什么?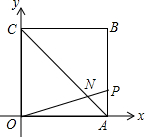 如图,点A(4,0),C(0,4)在平面直角坐标系中,将△AOC关于AC作轴对称得△ABC.动点P从点A出发,沿折线A→B→C运动至点C停止.连接OP,交AC于点N,则当△AON为等腰三角形时,点P的坐标是
如图,点A(4,0),C(0,4)在平面直角坐标系中,将△AOC关于AC作轴对称得△ABC.动点P从点A出发,沿折线A→B→C运动至点C停止.连接OP,交AC于点N,则当△AON为等腰三角形时,点P的坐标是