题目内容
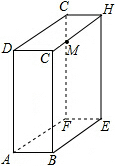 如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?考点:平面展开-最短路径问题
专题:分类讨论
分析:此题分两种情况比较最短距离:第一种是,先爬到DC棱的中点,再到M,此时转换到一个平面内,所走的路程是直角边为10cm、25cm的直角三角形的斜边的长;
第二种是,先抓到BC棱的中点,再到M,此时转换到一个平面人,所走的路程是直角边为15cm,20cm的直角三角形的斜边的长;再根据勾股定理求出AM的长,比较出其大小即可.
第二种是,先抓到BC棱的中点,再到M,此时转换到一个平面人,所走的路程是直角边为15cm,20cm的直角三角形的斜边的长;再根据勾股定理求出AM的长,比较出其大小即可.
解答: 解:分两种情况比较最短距离:
解:分两种情况比较最短距离:
如图1所示,
AM=
=5
如图2所示,
AM=
=25.
∵5
>25,
∴第二种短些,此时最短距离为25cm.
答:需要爬行的最短距离是25cm.
 解:分两种情况比较最短距离:
解:分两种情况比较最短距离:如图1所示,
AM=
| 102+(20+5)2 |
| 29 |
如图2所示,
AM=
| 202+(10+5)2 |
∵5
| 29 |
∴第二种短些,此时最短距离为25cm.
答:需要爬行的最短距离是25cm.
点评:本题考查的是平面展开-最短路径问题,根据题意画出图形,再根据勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、1的平方根是1 | ||
| B、0的平方根是0 | ||
C、2的算术平方根是
| ||
| D、-1的立方根是-1 |
 如图,在Rt△ABC中,AB=4,BC=3,在Rt△FAC中,AF=12,求正方形CDEF的面积.
如图,在Rt△ABC中,AB=4,BC=3,在Rt△FAC中,AF=12,求正方形CDEF的面积.