Question

3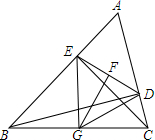．如图，在△ABC中，BD、CE是高，G、F分别是BC、DE的中点，则下列结论中错误的是（　　）

• A． GE=GD
• B． GF⊥DE
• C． GF平分∠DGE
• D． ∠DGE=60°

Answer 1

分析 利用直角三角形中，斜边上的中线等于斜边的一半，可得GE=$\frac{1}{2}$BC，GD=$\frac{1}{2}$BC，由此判定A正确；利用等腰三角形三线合一的性质可得FG⊥DE，GF平分∠DGE，由此判断B、C正确；根据已知条件不能得出∠DGE=60°，由此判断D错误．

解答 解：∵BD、CE是△ABC的高，G是BC的中点，
∴GE=$\frac{1}{2}$BC，GD=$\frac{1}{2}$BC，
∴GE=GD，故A选项正确；
∵GE=GD，F是DE的中点，
∴GF⊥DE，GF平分∠DGE，故B、C选项都正确；
根据已知条件不能得出△DGE是等边三角形，即∠DGE不一定是60°，故D选项错误．
故选D．

点评 本题考查了直角三角形斜边上的中线的性质，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键．同时考查了等腰三角形三线合一的性质．