题目内容
4.在两个等腰三角形ABC和A′B′C′中,∠A、∠A′分别是顶角,试分别依据下列条件,判断△ABC△A′B′C′是否相似?如果相似,请写出证明过程.(1)∠A=∠A′;
(2)∠B=∠B′(或∠C=∠C′)
分析 (1)由等腰三角形的性质得出∠B=∠C,∠B′=∠C′,由顶角相等和三角形内角和定理得出∠B=∠C=∠B′=∠C′,即可得出△ABC∽△A′B′C′;
(2)由等腰三角形的性质得出∠B=∠C,∠B′=∠C′,再由∠B=∠B′(或∠C=∠C′),得出∠C=∠C′(或∠B=∠B′),即可得出结论.
解答 证明:(1)∵△ABC和△A′B′C′是等腰三角形,∠A、∠A′分别是顶角,
∴∠B=∠C,∠B′=∠C′,
∵∠A=∠A′,∠A+∠B+∠C=180°,∠A′+∠B′+∠C′=180°,
∴∠B=∠C=∠B′=∠C′,
∴△ABC∽△A′B′C′;
(2)∵△ABC和△A′B′C′是等腰三角形,∠A、∠A′分别是顶角,
∴∠B=∠C,∠B′=∠C′,
∵∠B=∠B′,
∴∠C=∠C′,
∴△ABC∽△A′B′C′;
若∠C=∠C′,
同理可证:△ABC∽△A′B′C′.
点评 本题考查了相似三角形的判定方法、等腰三角形的性质、三角形内角和定理;熟练掌握相似三角形的判定方法,弄清等腰三角形的角之间的关系是解决问题的关键.

练习册系列答案
相关题目
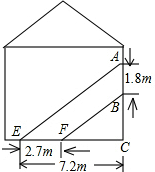 如图,阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区,已知亮区到窗口下的墙脚距离EC=7.2m,窗口高AB=1.8m.求窗口底边离地面的高BC.
如图,阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区,已知亮区到窗口下的墙脚距离EC=7.2m,窗口高AB=1.8m.求窗口底边离地面的高BC.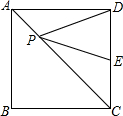 正方形ABCD中,点P是对角线AC上的动点,点E是CD的中点,AB=2,求PD+PE的最小值.
正方形ABCD中,点P是对角线AC上的动点,点E是CD的中点,AB=2,求PD+PE的最小值.