题目内容
5. 如图,在正方形ABCD中,AB=4,BD是对角线.将△DCB绕着D点逆时针旋转α(90°<α<180°),得到△DEF,连接BF,CE相交于G点,EG=1,则BF=$\sqrt{62}$+$\sqrt{2}$.
如图,在正方形ABCD中,AB=4,BD是对角线.将△DCB绕着D点逆时针旋转α(90°<α<180°),得到△DEF,连接BF,CE相交于G点,EG=1,则BF=$\sqrt{62}$+$\sqrt{2}$.
分析 作EH⊥BF于H,连接DG,CE交BD于O.首先证明DG⊥BF,推出FG=BG,求出FG即可解决问题.
解答 解:作EH⊥BF于H,连接DG,CE交BD于O.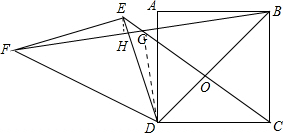
∵∠EDC=90°+∠ADE,∠BDF=90°+∠ADE,
∴∠EDC=∠FDB,
∵DF=DB,CD=DE,
∴∠DFB=∠DBF=∠DCE=∠DEC,
∵∠BOG=∠DOC,
∴△BOG∽△COD,
∴$\frac{OG}{OD}$=$\frac{OB}{OC}$,∠ODC=∠OGB=45°
∴$\frac{OG}{OB}$=$\frac{OD}{OC}$,
∴△GOD∽△BOC,
∴∠DGO=∠OBC=45°,
∴∠DGB=90°,
∵DF=DB,
∴FG=BG,
在Rt△EHG中,∵∠EGH=∠BGO=45°,EG=1,
∴EH=HG=$\frac{\sqrt{2}}{2}$,
在Rt△EFH中,∵EF=4,EH=$\frac{\sqrt{2}}{2}$,
∴FH=$\sqrt{E{F}^{2}-E{H}^{2}}$=$\frac{\sqrt{62}}{2}$,
∴FG=BG=$\frac{\sqrt{62}+\sqrt{2}}{2}$,
∴BF=$\sqrt{62}$+$\sqrt{2}$.
故答案为$\sqrt{62}$+$\sqrt{2}$.
点评 本题考查正方形的性质、相似三角形的判定和性质、等腰三角形的性质、勾股定理的等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考填空题中的压轴题.

练习册系列答案
相关题目
15.西峡民兵训练,一列队长200m的军队匀速通过一条长0.8km的鹳河大桥,测得军队通过大桥用时8min,(计算结果小数点后保留2位)求:
(1)军队前进的速度;
(2)这列军队全部在大桥上行走的时间.
(1)军队前进的速度;
(2)这列军队全部在大桥上行走的时间.
10.某射击运动员在同一条件下进行射击,结果如表所示:
(1)完成表格;
(2)根据表格,画出该运动员击中靶心的频率的折线统计图;
(3)观察画出的折线统计图,击中靶心的频率的变化有什么规律?
| 射击总次数n | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
| 击中靶心次数m | 9 | 16 | 41 | 88 | 168 | 429 | 861 |
| 击中靶心频率 $\frac{m}{n}$ | 0.9 | 0.8 | 0.82 | 0.88 | 0.84 | 0.858 | 0.861 |
(2)根据表格,画出该运动员击中靶心的频率的折线统计图;
(3)观察画出的折线统计图,击中靶心的频率的变化有什么规律?
17.己知抛物线y=x2-2(m+3)x+n,与x轴只有一个交点,抛物线上有三点A(m+6,y1)、B(0,y2)、C(m,y3)且m>0则y1、y2、y3关系为( )
| A. | y1=y3<y2 | B. | y1>y2>y3 | C. | y1>y3<y2 | D. | y2>y1>y3 |
15.计算4-(-5)的结果是( )
| A. | 9 | B. | 1 | C. | -1 | D. | -9 |
