题目内容
3．如果|2x+2|与$\sqrt{y-3}$互为相反数，则xy为（ ）| A． | 2 | B． | -2 | C． | 3 | D． | -3 |
分析 根据互为相反数的两个数的和等于0列方程，再根据非负数的性质列方程求出x、y的值，然后相乘计算即可得解．
解答 解：∵|2x+2|与$\sqrt{y-3}$互为相反数，
∴|2x+2|+$\sqrt{y-3}$=0，
∴2x+2=0，y-3=0，
解得x=-1，y=3，
所以，xy=（-1）×3=-3．
故选D．
点评 本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
相关题目
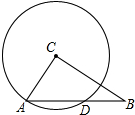如图，△ABC中，∠ACB=90°，CA=15cm，CB=20cm，以CA为半径的⊙C交AB于D，求AD的长．
，其中x=－2．
个单位长度的速度沿射线AB方向运动，过点P作PQ⊥AB，交x轴于点Q，PR∥AC交x轴于点R，设点P运动时间为t（秒），线段QR长为d，求d与t的函数关系式（不要求写出自变量t的取值范围）；