题目内容
14.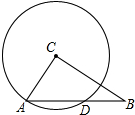 如图,△ABC中,∠ACB=90°,CA=15cm,CB=20cm,以CA为半径的⊙C交AB于D,求AD的长.
如图,△ABC中,∠ACB=90°,CA=15cm,CB=20cm,以CA为半径的⊙C交AB于D,求AD的长.
分析 先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长,在Rt△ACM中,根据勾股定理可求出AM的长,进而可得出结论.
解答  解:∵在Rt△ABC中,∠ACB=90°,AC=8,BC=15,
解:∵在Rt△ABC中,∠ACB=90°,AC=8,BC=15,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{1{5}^{2}+2{0}^{2}}$=25.
过C作CM⊥AB,交AB于点M,如图所示,
∵CM⊥AB,
∴M为AD的中点,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CM,且AC=15,BC=20,AB=25,
∴CM=$\frac{15×20}{25}$=12,
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即225=AM2+144,
解得:AM=9,
∴AD=2AM=18.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
6.2016年10月17日,神州十一号载人飞船上天,到达距离地面393公里轨道的新高度,我国开始实施航天员中期驻留试验,目前在轨飞行速度约为7820米/秒,其中数据7820用科学记数法表示为( )
| A. | 7.8×103 | B. | 78.2×102 | C. | 7.82×103 | D. | 7.82×104 |
6.若y=$\frac{9}{2}$,则$\frac{2x+6}{12y}$÷$\frac{x+3}{12{y}^{2}}$的结果为( )
| A. | 6 | B. | 9 | C. | $\frac{9}{2}$ | D. | $\frac{81}{4}$ |
3.在有理数-2,0,2,3中,最小的数是( )
| A. | -2 | B. | 0 | C. | 2 | D. | 3 |
19.两个互为相反数的有理数相除,商为( )
| A. | 正数 | B. | 负数 | C. | 不存在 | D. | 负数或不存在 |
6.已知地球上海洋面积约为361000000km2,361000000用科学记数法可以表示为( )
| A. | 36.1×107 | B. | 3.61×107 | C. | 3.61×108 | D. | 3.61×109 |
3.杭州地铁7号线预计2022年亚运会前开通,7号线全长约45.1千米,45.1千米用科学记数法表示为( )
| A. | 4.51×104米 | B. | 45.1×104米 | C. | 4.51×105米 | D. | 4.51×103米 |
3.如果|2x+2|与$\sqrt{y-3}$互为相反数,则xy为( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
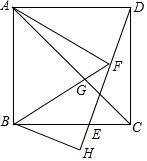 在正方形ABCD中,点E为BC边上的一点,连接DE,点F为DE的中点,连接FA、FB,线段FB与AC交于点G,过B作BH⊥DE交DE的延长线于点H,若BH=3,AG:GC=$\sqrt{3}$:1,则△AFG的面积为9$\sqrt{3}$-$\frac{27}{2}$.
在正方形ABCD中,点E为BC边上的一点,连接DE,点F为DE的中点,连接FA、FB,线段FB与AC交于点G,过B作BH⊥DE交DE的延长线于点H,若BH=3,AG:GC=$\sqrt{3}$:1,则△AFG的面积为9$\sqrt{3}$-$\frac{27}{2}$.