题目内容
如图，已知△ABC为等边三角形，BD为中线，延长BC至E，使CE=CD，连接DE，则∠BDE=考点：等边三角形的性质,等腰三角形的性质
专题：
分析：由△ABC为等边三角形，可求出∠BDC=90°，由△DCE是等腰三角形求出∠CDE=∠CED=30°，即可求出∠BDE的度数．
解答：解：∵△ABC为等边三角形，BD为中线，
∴∠BDC=90°，∠ACB=60°
∴∠ACE=180°-∠ACB=180°-60°=120°，
∵CE=CD，
∴∠CDE=∠CED=30°，
∴∠BDE=∠BDC+∠CDE=90°+30°=120°，
故答案为：120．
∴∠BDC=90°，∠ACB=60°
∴∠ACE=180°-∠ACB=180°-60°=120°，
∵CE=CD，
∴∠CDE=∠CED=30°，
∴∠BDE=∠BDC+∠CDE=90°+30°=120°，
故答案为：120．
点评：本题主要考查了等边三角形的性质及等腰三角形的性质，解题的关键是熟记等边三角形的性质及等腰三角形的性质．
练习册系列答案
相关题目
如图，△ABC中，AB=AC，BD和CE分别是∠ABC和∠ACB的角平分线．则△ABD和哪个三角形全等？为什么？△BEC和哪个三角形全等？为什么？
在数学校本活动课上，张老师设计了一个游戏，让电动娃娃在边长为1的正方形的四个顶点上依次跳动．规定：从顶点A出发，每跳动一步的长均为1．第一次顺时针方向跳1步到达顶点D，第二次逆时针方向跳2步到达顶点B，第三次顺时针方向跳3步到达顶点C，第四次逆时针方向跳4步到达顶点C，…，以此类推，跳动第2013次到达的顶点是
如图，P是正方形ABCD内任意一点，△APD与△BPC的面积之和为8cm2，则AB=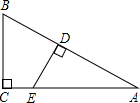
在Rt△ABC中，∠C=90°，∠A=30°，点D，E分别在AB，AC上，若DE将△ABC分成面积相等的两部分，且△ABC的面积为20，AE=8，则AD=