题目内容
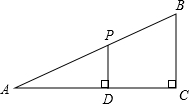 如图,在Rt△ABC中,∠C=90°,BC=6,D是AC边长一动点,过点D作DP∥BC交AB于P.
如图,在Rt△ABC中,∠C=90°,BC=6,D是AC边长一动点,过点D作DP∥BC交AB于P.(1)当D在AC上运动时(不考虑与A、C重合的情形),∠APD的余弦值是否会发生变化?为什么?
(2)当AD=5,BC=6且PD:AC=1:3时,求cosA.
考点:解直角三角形
专题:
分析:(1)可证∠APD的大小不会变化,即可解题;
(2)可证△APD∽△ABC,即可得PD•AC的值,即可求得PD的值,即可解题.
(2)可证△APD∽△ABC,即可得PD•AC的值,即可求得PD的值,即可解题.
解答:解:(1)∵DP∥BC,
∴∠APD=∠ABC,
当D在AC上运动时(不考虑与A、C重合的情形),∠APD的大小不会变化,所以∠APD的余弦值不会变化.
(2)∵DP∥BC,
∴△APD∽△ABC,
∴
=
,即PD•AC=30,
∵PD:AC=1:3,
∴PD=
,
∴AP=
=
,
∴cosA=
=
.
∴∠APD=∠ABC,
当D在AC上运动时(不考虑与A、C重合的情形),∠APD的大小不会变化,所以∠APD的余弦值不会变化.
(2)∵DP∥BC,
∴△APD∽△ABC,
∴
| PD |
| BC |
| AD |
| AC |
∵PD:AC=1:3,
∴PD=
| 10 |
∴AP=
| AD2+PD2 |
| 35 |
∴cosA=
| 5 | ||
|
| ||
| 7 |
点评:本题考查了直角三角形中勾股定理的运用,考查了相似三角形对应边比例相等的性质,本题中求证△APD∽△ABC是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
化简
-
(
+2)得( )
| 8 |
| 2 |
| 2 |
| A、-2 | ||
B、
| ||
| C、2 | ||
D、4
|
已知样本数据1、2、4、3、5,下列说法不正确的是( )
| A、极差是4 | B、平均数是3 |
| C、中位数是4 | D、方差是2 |
下列线段的长度能围成三角形的是( )
| A、1cm,2cm,3cm |
| B、2cm,5cm,3cm |
| C、3cm,4cm,5cm |
| D、4cm,4cm,9cm. |
 如图所示圆柱形玻璃容器,高17cm,底面周长为24cm,在外侧下底面点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇,急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度是( )
如图所示圆柱形玻璃容器,高17cm,底面周长为24cm,在外侧下底面点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇,急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度是( )| A、20cm | ||
B、8
| ||
C、
| ||
| D、24cm |
 ?根据2014年11月份的月历表,思考并回答如下问题:
?根据2014年11月份的月历表,思考并回答如下问题: