题目内容
观察下列各式2=2,2+4=6,2+4+6=12,2+4+6+8=20,2+4+6+8+10=30,…根据上述算式中的规律你认为第n个式子为 .
考点:规律型:数字的变化类
专题:规律型
分析:根据从2开始的连续偶数的和等于两个连续自然数的乘积解答即可.
解答:解:∵2=2=1×2,
2+4=6=2×3,
2+4+6=12=3×4,
2+4+6+8=20=4×5,
2+4+6+8+10=30=5×6,
…,
∴第n个式子为2+4+6+8+10+…+2n=n(n+1).
故答案为:2+4+6+8+10+…+2n=n(n+1).
2+4=6=2×3,
2+4+6=12=3×4,
2+4+6+8=20=4×5,
2+4+6+8+10=30=5×6,
…,
∴第n个式子为2+4+6+8+10+…+2n=n(n+1).
故答案为:2+4+6+8+10+…+2n=n(n+1).
点评:本题是对数字变化规律的考查,观察出从2开始的连续偶数的和等于两个连续自然数的积是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知实数x,y满足
+|y+1|=0,则x-y等于( )
| x-2 |
| A、3 | B、-3 | C、1 | D、-1 |
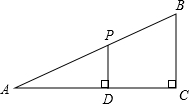 如图,在Rt△ABC中,∠C=90°,BC=6,D是AC边长一动点,过点D作DP∥BC交AB于P.
如图,在Rt△ABC中,∠C=90°,BC=6,D是AC边长一动点,过点D作DP∥BC交AB于P.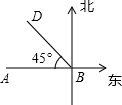 由于过度采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭,近日,A市气象局测得沙尘暴中心在A市的正东方向400km的B处,正在以50
由于过度采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭,近日,A市气象局测得沙尘暴中心在A市的正东方向400km的B处,正在以50 如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,CD=3.
如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,CD=3.