题目内容
在圆O中,圆心O离弦AB距离等于弦长的一半,该弦所对的弧长是47π,求圆O半径.
考点:弧长的计算
专题:
分析:根据题意画出图形,可能是劣弧为47π,也可能是优弧为47π,如图所示,由OA=OB,OD垂直于AB,得到OD为角平分线,在直角三角形AOD中,由OD为AB的一半,得到∠OAD的度数,进而求出∠AOD的度数,即可求出∠AOB的度数,从而得出OA的长.
解答: 解:∵OA=OB,OD⊥AB,
解:∵OA=OB,OD⊥AB,
∴OD平分∠AOB,即∠AOD=∠BOD,
在Rt△AOD中,OD=
AB,
∴∠OAD=45°,∠AOD=45°,
则∠AOB=2∠AOD=90°.
①∵劣弧为47π,
∴
=47π,
∴OA=94,
②∵优弧为47π,
∴
=47π,
∴OA=
.
 解:∵OA=OB,OD⊥AB,
解:∵OA=OB,OD⊥AB,∴OD平分∠AOB,即∠AOD=∠BOD,
在Rt△AOD中,OD=
| 1 |
| 2 |
∴∠OAD=45°,∠AOD=45°,
则∠AOB=2∠AOD=90°.
①∵劣弧为47π,
∴
| 90π•OA |
| 180 |
∴OA=94,
②∵优弧为47π,
∴
| 270π•OA |
| 180 |
∴OA=
| 94 |
| 3 |
点评:本题考查了弧长的计算,以及垂径定理,等腰三角形的性质,含30度角的直角三角形,熟练掌握定理及性质是解本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
在-1
,12,-20,0,-(-5)中,负数的个数有( )
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
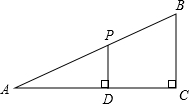 如图,在Rt△ABC中,∠C=90°,BC=6,D是AC边长一动点,过点D作DP∥BC交AB于P.
如图,在Rt△ABC中,∠C=90°,BC=6,D是AC边长一动点,过点D作DP∥BC交AB于P. 如图,有一圆柱,其高为12cm,它的底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为( )cm.(π取3)
如图,有一圆柱,其高为12cm,它的底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为( )cm.(π取3)