题目内容
18．
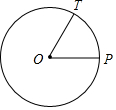如图，OP是⊙O的半径，∠POT=60°，OT交⊙O于点S．（1）过点P作⊙O的切线；
（2）过点P的切线交OT于点Q，判断点S是不是线段OQ的中点，并说明理由．
分析 （1）过点P作PO的垂线即可；
（2）依据含30°直角三角形的性质求解即可．
解答 解：（1）如图所示
QP即为所求作的切线．
（2）∵∠TOP=60°，∠OPQ=90°，
∴∠OQP=30°．
∴OP=$\frac{1}{2}$OQ．
∵OS=OP，
∴OS=$\frac{1}{2}$OQ．
∴S是线段OQ的中点．
点评 本题主要考查的是切线的性质、含30°直角三角形的性质，熟练掌握相关知识是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
作图题：（不要求写作法）如图，△ABC在平面直角坐标系中，其中，点A，B，C的坐标分别为A（-2，1），B（-4，5），C（-5，2）．
如图，已知点C在线段AB上，且AC=6cm，BC=4cm，点M，N分别是AC，BC的中点，则MN的值是5cm．
如图，在5×4的方格纸中，每个小正方形边长为1，点O，A，B在方格纸的交点（格点）上，在第四象限内的格点上找点C，使△ABC的面积为3，则这样的点C共有5个．
如图，∠A=∠C，∠1=∠2．求证：AB=CD．