题目内容
2.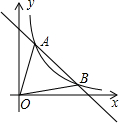 如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数y=$\frac{k}{x}$(k≠0)的值时,写出自变量x的取值范围.
分析 (1)将点A 的横坐标代入直线的解析式求出点A的坐标,然后将的A的坐标代入反比例函数的解析式即可.
(2)一次函数y=-x+5的值大于反比例函数y=$\frac{k}{x}$(k≠0)的值时,双曲线便在直线的下方,所以求出直线与双曲线及x轴的交点后可由图象直接写出其对应的x取值范围.
解答 解:(1)∵点A(1,n)在一次函数y=-x+5的图象上,
∴当x=1时,y=-1+5=4
即:A点的坐标为:(1,4)
∵点A(1,4)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上
∴k=1×4=4,
∴反比例函数的解析式为:y=$\frac{4}{x}$;
(2)如下图所示:
解方程组:$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=-x+5}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$
∴B点的坐标为(4,1)
直线与x轴的交点C为(5,0)
由图象可知:当 1<x<4时一次函数y=-x+5的值大于反比例函数y=$\frac{k}{x}$(k≠0)的值.
点评 本题考查了反比例函数与一次函数的交点问题,解题的关键是掌握反比例函数与一次函数的交点与它们的解析式的关系.

练习册系列答案
相关题目
13.已知⊙O的半径为2cm,弦AB长为2cm,则这条弦的中点到弦所对优弧中点的距离为( )
| A. | 2cm | B. | $\sqrt{3}$cm | C. | (2-$\sqrt{3}$)cm | D. | (2+$\sqrt{3}$)cm |
14.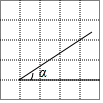 在5×5网格中,∠α的位置如图所示,则tanα的值是( )
在5×5网格中,∠α的位置如图所示,则tanα的值是( )
 在5×5网格中,∠α的位置如图所示,则tanα的值是( )
在5×5网格中,∠α的位置如图所示,则tanα的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
12.若|a|=1,则a=( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 0 |
 已知CD是Rt△ABC斜边上的高线,且AB=10,若BC=8,则cos∠ACD=$\frac{4}{5}$.
已知CD是Rt△ABC斜边上的高线,且AB=10,若BC=8,则cos∠ACD=$\frac{4}{5}$.


