题目内容

13．已知⊙O的半径为2cm，弦AB长为2cm，则这条弦的中点到弦所对优弧中点的距离为（　　）
A．2cmB．$\sqrt{3}$cmC．（2-$\sqrt{3}$）cmD．（2+$\sqrt{3}$）cm

分析 连接OA，根据垂径定理得出CD过O，AD=BD=1cm，OD⊥AB，根据勾股定理求出OD长，即可求出CD．

解答 解：连接OA，
∵D为AB中点，OD过圆心O，C为$\widehat{ACB}$的中点，
∴由垂径定理得：CD过O，AD=BD=1cm，OD⊥AB，
∵在△ODA中，OA=2cm，AD=1cm，
由勾股定理得：OD=$\sqrt{3}$cm，
∴CD=OC+OD=（2+$\sqrt{3}$）cm，
故选：D．

点评 本题考查了勾股定理和垂径定理的应用，解此题的关键是构造直角三角形、灵活运用垂径定理和勾股定理求出OD长．

练习册系列答案
相关题目
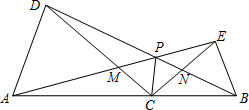5．如图，C为线段AB上的任意一点（不与点A，B重合），分别以AC，BC为一腰在AB的同侧作等腰三角形ACD和等腰三角形BCE，CA=CD，CB=CE，∠ACD与∠BCE都是锐角且∠ACD=∠BCE，连接AE交CD于点M，连接BD交CE于点N，AE与BD相交于点P，连接PC．求证：△ACE≌△DCB．
4．设N=88888888写成十进制数时，它的各位数字之和是A，而A的各位数字之和是B，B的各位数字之和是C．则C是（　　）
A．11B．7C．9D．4
1．若abc＞0，化简$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$+$\frac{abc}{|abc|}$结果是4或0．
8．据报道，2016年初我国网民规模达719 000 000人，将这个数用科学记数法表示为（　　）
A．7.19×109B．7.19×108C．71.9×107D．0.719×109
18．某车间有22名工人生产眼镜，1名工人每天生产2000片镜片或1200个镜架，应如何分配工人生产镜片和镜架，才能使每天生产的产品配套？
5．下列方程中，是一元二次方程的是（　　）
A．2x-y=3B．x2+$\frac{1}{x}$=2C．x2+1=x2-1D．x（x-1）=0
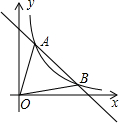2．如图，一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$（k≠0）在第一象限的图象交于A（1，n）和B两点．
（1）求反比例函数的解析式及点B坐标；
（2）在第一象限内，当一次函数y=-x+5的值大于反比例函数y=$\frac{k}{x}$（k≠0）的值时，写出自变量x的取值范围．
3．化简下列各数：
（1）+（-2）=-2；              
（2）-（+3）=-3；
（3）-（+10）=-10；           
（4）+（-0.15）=-0.15；
（5）|-（+$\frac{1}{2}$）|=$\frac{1}{2}$；            
（6）-|-1$\frac{1}{3}$|=-1$\frac{1}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网