题目内容
7．
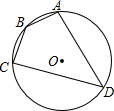如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠B=135°，则$\widehat{AC}$的长（ ）| A． | 2π | B． | π | C． | $\frac{π}{2}$ | D． | $\frac{π}{3}$ |
分析 连接OA、OC，然后根据圆周角定理求得∠AOC的度数，最后根据弧长公式求解．
解答 解：
连接OA、OC，
∵∠B=135°，
∴∠D=180°-135°=45°，
∴∠AOC=90°，
则$\widehat{AC}$的长=$\frac{90π×2}{180}$=π．
故选B．
点评 本题考查了弧长的计算以及圆周角定理，解答本题的关键是掌握弧长公式L=$\frac{nπR}{180}$．
练习册系列答案
相关题目
17．下列说法中正确的是（ ）
| A． | “打开电视机，正在播放《动物世界》”是必然事件 | |
| B． | 某种彩票的中奖概率为$\frac{1}{1000}$，说明每买1000张，一定有一张中奖 | |
| C． | 抛掷一枚质地均匀的硬币一次，出现正面朝上的概率为$\frac{1}{3}$ | |
| D． | 想了解长沙市所有城镇居民的人均年收入水平，宜采用抽样调查 |
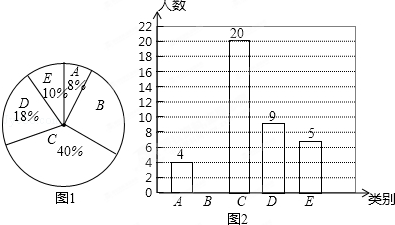
15．
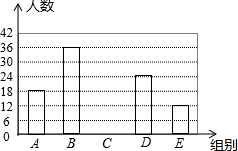随着我市社会经济的发展和交通状况的改善，我市的旅游业得到了高速发展，某旅游公司对我市一企业旅游年消费情况进行了问卷调查，随机抽取部分员工，记录每个人消费金额，并将调查数据适当调整，绘制成如图两幅尚不完整的表和图．
根据以上信息回答下列问题：
（1）a=36，b=0.30，c=120．并将条形统计图补充完整；
（2）这次调查中，个人年消费金额的中位数出现在C组；
（3）若这个企业有3000多名员工，请你估计个人旅游年消费金额在6000元以上的人数．
随着我市社会经济的发展和交通状况的改善，我市的旅游业得到了高速发展，某旅游公司对我市一企业旅游年消费情况进行了问卷调查，随机抽取部分员工，记录每个人消费金额，并将调查数据适当调整，绘制成如图两幅尚不完整的表和图．| 组别 | 个人年消费金额x（元） | 频数（人数） | 频率 |
| A | x≤2000 | 18 | 0.15 |
| B | 2000＜x≤4000 | a | b |
| C | 4000＜x≤6000 | ||
| D | 6000＜x≤8000 | 24 | 0.20 |
| E | x＞8000 | 12 | 0.10 |
| 合计 | c | 1.00 | |
（1）a=36，b=0.30，c=120．并将条形统计图补充完整；
（2）这次调查中，个人年消费金额的中位数出现在C组；
（3）若这个企业有3000多名员工，请你估计个人旅游年消费金额在6000元以上的人数．
2．
有6个相同的立方体搭成的几何体如图所示，则它的主视图是（ ）
有6个相同的立方体搭成的几何体如图所示，则它的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
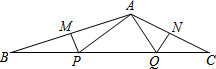如图，△ABC中，∠BAC=135°，点P、Q在边BC上，若MP和QN分别垂直平分AB和AC，并且AP=8，AQ=6，求BC的长．