题目内容
10.${x^2}-\frac{b}{a}x$+$\frac{{b}^{2}}{4{a}^{2}}$=(x-$\frac{b}{2a}$)2.分析 直接配上一次项系数的一半的平方,即可变为完全平方式.
解答 解:${x^2}-\frac{b}{a}x$+$\frac{{b}^{2}}{4{a}^{2}}$=(x-$\frac{b}{2a}$).
故答案为:$\frac{{b}^{2}}{4{a}^{2}}$,$\frac{b}{2a}$.
点评 本题考查了配方法的应用:配方法的理论依据是公式a2±2ab+b2=(a±b)2.二次三项式是完全平方式,则常数项是一次项系数一半的平方.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
18.如果x=$\frac{1}{2}$是关于x的方程2x2+3ax-2a=0的根,那么关于y的方程y2-3=a的解是( )
| A. | ±$\sqrt{5}$ | B. | ±1 | C. | ±2 | D. | ±$\sqrt{2}$ |
15.方程mx2-4x+1=0(m<0)的根是( )
| A. | $\frac{1}{4}$ | B. | $\frac{{2±\sqrt{4-m}}}{m}$ | C. | $\frac{{2±2\sqrt{4-m}}}{m}$ | D. | $\frac{{2±m\sqrt{4-m}}}{m}$ |
2.关于x的一元二次方程$\sqrt{2}{x^2}+\sqrt{2}{a^2}=3ax$的两根应为( )
| A. | $\frac{{-\sqrt{2}±a}}{{\sqrt{2}}}$ | B. | $\sqrt{2}a$,$\frac{{\sqrt{2}}}{2}a$ | C. | $\frac{{2±\sqrt{2}a}}{4}$ | D. | $±\sqrt{2}a$ |
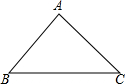 如图.张大爷家有一个三角形鱼塘,A,B,C三处分别栽有一棵树.现要扩大鱼塘面积,且将鱼塘改为圆形,并保留三棵树的位置不动,使鱼塘的面积最大,请你设计鱼塘的位置.
如图.张大爷家有一个三角形鱼塘,A,B,C三处分别栽有一棵树.现要扩大鱼塘面积,且将鱼塘改为圆形,并保留三棵树的位置不动,使鱼塘的面积最大,请你设计鱼塘的位置.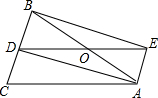 如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O是AB的中点,连接DO并延长到E,使DO=EO,连接AE,BE.
如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O是AB的中点,连接DO并延长到E,使DO=EO,连接AE,BE. 如图,△ABC∽△DEF,若∠B=50°,则∠E的度数是50度.
如图,△ABC∽△DEF,若∠B=50°,则∠E的度数是50度.