题目内容
 如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE.
如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE.(1)求证:AE=CF;
(2)求证:AE∥CF.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)易证BE=DF,即可求证△ABE≌△CDF,即可解题;
(2)根据(1)中的△ABE≌△CDF可得∠AEB=∠CFD,即可解题.
(2)根据(1)中的△ABE≌△CDF可得∠AEB=∠CFD,即可解题.
解答:解:(1)∵BF=DE,
∴BF+EF=DE+EF,
即BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=CF;
(2)由(1)知:△ABE≌△CDF,
∴∠AEB=∠CFD,
∴AE∥CF.
∴BF+EF=DE+EF,
即BE=DF,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(SAS),
∴AE=CF;
(2)由(1)知:△ABE≌△CDF,
∴∠AEB=∠CFD,
∴AE∥CF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABE≌△CDF是解题的关键.

练习册系列答案
相关题目
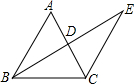 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=56°,则∠E=( )
如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=56°,则∠E=( )| A、27° | B、28° |
| C、26° | D、30° |
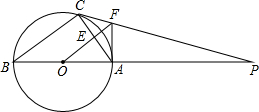 如图,△ABC内接⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,若AC=24,AF=15,求圆的半径.
如图,△ABC内接⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,若AC=24,AF=15,求圆的半径. 如图,△ABC中,DE∥BC,EF∥AB.
如图,△ABC中,DE∥BC,EF∥AB.