题目内容
9.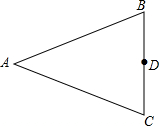 如图,在△ABC中,AB=AC,D是BC上的任意一点.
如图,在△ABC中,AB=AC,D是BC上的任意一点.(1)过A、B、D三点作⊙O,交线段AC于点E(用直尺和圆规作图,保留作图痕迹,不写作法);
(2)若$\widehat{DE}$=$\widehat{DB}$,求证:AB是⊙O的直径;
(3)在(2)的条件下,若AB=13,BC=10,求AE的长.
分析 (1)作AB与BD的垂线,交于点O,点O就是△ABD的外心,⊙O交线段AC于点E;
(2)连结DE,根据圆内接四边形的性质,等腰三角形的性质,即可得到AD是等腰三角形ABC底边上的高线,从而证明AB是⊙O的直径;
(3)连结BE,根据勾股定理得到关于AE的方程,解方程即可求解.
解答 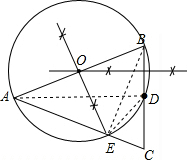 (1)解:如图,⊙O即为所求;
(1)解:如图,⊙O即为所求;
(2)证明:∵过A、B、D三点作⊙O,交线段AC于点E,
∴A、B、D、E四点共圆,
∴∠DEC=∠ABC,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠DEC=∠ACB,
∴DE=CD,
∵$\widehat{DE}$=$\widehat{DB}$,
∴DE=BD,
∴CD=BD,
∴AD⊥BC,
∴AB是⊙O的直径;
(3)解:连结BE,
∵AB是⊙O的直径,
∴BE⊥AC,
由勾股定理可得,AB2-AE2=BC2-(AC-AE)2,即132-AE2=102-(13-AE)2,
解得AE=$\frac{119}{13}$.
故AE的长是$\frac{119}{13}$.
点评 此题考查的是作图-复杂作图,线段垂直平分线的作法,圆内接四边形的性质,等腰三角形的性质,勾股定理,方程思想的应用.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
20.将图1中的正方形剪开得到图2,则图2 中共有4个正方形;将图2中的一个正方形剪开得到图3,则图3中共有7个正方形;…,如此剪下去,则第n个图形中正方形的个数是多少.
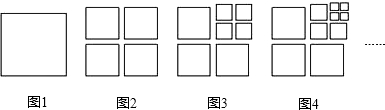
(1)按图示规律填写下表:
(2)按照这种方式剪下去,求第n个图中有多少个正方形;
(3)按照这种方式剪下去,求第200个图中有多少个正方形;
(4)按照这种方式剪下去,求第2017个图中有多少个正方形.

(1)按图示规律填写下表:
| 图 | 1 | 2 | 3 | 4 | 5 | … |
| 正方形个数 | 1 | 4 | 7 | 10 | 13 | … |
(3)按照这种方式剪下去,求第200个图中有多少个正方形;
(4)按照这种方式剪下去,求第2017个图中有多少个正方形.
17.点(-2,4)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,则该函数的图象位于第( ) 象限.
| A. | 一、三 | B. | 二、四 | C. | 一、四 | D. | 二、三 |
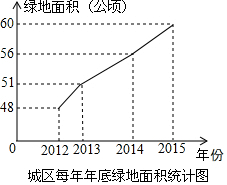 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).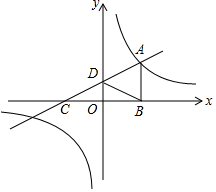 如图,直线y=$\frac{1}{2}$x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点A(m,2),与x轴交于点C,与y轴交于点D,过A作AB⊥x轴于点B,连接BD.
如图,直线y=$\frac{1}{2}$x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点A(m,2),与x轴交于点C,与y轴交于点D,过A作AB⊥x轴于点B,连接BD. 如图,四边形ABCD是长方形,AC为长方形对角线,画出与△ABC关于AC成轴对称的图形.
如图,四边形ABCD是长方形,AC为长方形对角线,画出与△ABC关于AC成轴对称的图形.