题目内容
13.(1)先化简:$\frac{{x}^{2}}{x-1}$+$\frac{1}{1-x}$;并从-1,0,1三个数中找出一个你喜欢的数代入求值;(2)已知x为整数,且$\frac{2}{x+3}$+$\frac{2}{3-x}$+$\frac{2x+18}{{x}^{2}-9}$的值为整数,求所有符合条件的x的值之和.
分析 (1)原式变形后,利用同分母分式的减法法则计算,约分得到最简结果,把x的值代入计算即可求出值;
(2)原式通分并利用同分母分式的加减法则计算,由x为整数,原式的值为整数确定出x的值,求出之和即可.
解答 解:(1)原式=$\frac{{x}^{2}-1}{x-1}$=x+1,
当x=0时,原式=1;
(2)原式=$\frac{2(x-3)-2(x+3)+2x+18}{(x+3)(x-3)}$=$\frac{2(x+3)}{(x+3)(x-3)}$=$\frac{2}{x-3}$,
由x为整数,原式结果为整数,得到x=1时,原式=-1;x=2时,原式=-2;x=4时,原式=2;x=5时,原式=1,
则所有符合条件x的值之和为1+2+4+5=12.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13-10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
(1)该市规定用水量为8吨,规定用量内的收费标准是2元/吨,超过部分的收费标准是3元/吨.
(2)若小明家五月份用水20吨,则应缴水费52元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
| 月份 | 一 | 二 | 三 | 四 |
| 用水量(吨) | 6 | 7 | 12 | 15 |
| 水费(元) | 12 | 14 | 28 | 37 |
(2)若小明家五月份用水20吨,则应缴水费52元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
8. 如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成9块,下面是四个计算种花土地总面积的代数式:①(a-2b)(a-2b),②a2-4ab,③a2-4ab-4b2,④a2-4ab+4b2,其中正确的有( )
如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成9块,下面是四个计算种花土地总面积的代数式:①(a-2b)(a-2b),②a2-4ab,③a2-4ab-4b2,④a2-4ab+4b2,其中正确的有( )
 如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成9块,下面是四个计算种花土地总面积的代数式:①(a-2b)(a-2b),②a2-4ab,③a2-4ab-4b2,④a2-4ab+4b2,其中正确的有( )
如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成9块,下面是四个计算种花土地总面积的代数式:①(a-2b)(a-2b),②a2-4ab,③a2-4ab-4b2,④a2-4ab+4b2,其中正确的有( )| A. | ② | B. | ①③ | C. | ①④ | D. | ④ |
某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
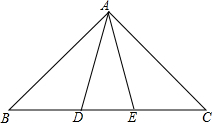 如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.
如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.