题目内容
3.(1)已知:如图1,AE∥CF,易知∠APC=∠A+∠C,请补充完整证明过程:证明:过点P作MN∥AE
∵MN∥AE(已作)
∴∠APM=∠A(两直线平行,内错角相等),
又∵AE∥CF,MN∥AE
∴MN∥CF
∴∠MPC=∠C(两直线平行,内错角相等)
∴∠APM+∠CPM=∠A+∠C
即∠APC=∠A+∠C
(2)变式:
如图2--图4,AE∥CF,P1,P2是直线EF上的两点,猜想∠A,∠AP1P2,∠P1P2C,∠C这四个角之间的关系,并直接写出以下三种情况下这四个角之间的关系.如图2,∠AP1P2+∠P1P2C-∠A-∠C=180°,如图3,∠A+∠AP1P2+∠P1P2C-∠C=180°,如图4,∠AP1P2+∠P1P2C-∠A+∠C=180°,

分析 (1)根据平行线的性质直接填空;
(2)如图2,过P1作P1B∥AE,过P2作P2G∥CF,先根据平行线性质得角相等,再根据∠AP1P2+∠P1P2C等量代换得出结论;
如图3,过P2作GP2∥CF,根据∠AP1P2+∠P1P2C等量代换得出结论;
如图4,过P1作P1G∥CF,根据∠AP1P2+∠P1P2C等量代换得出结论.
解答 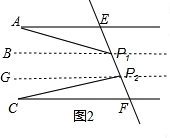 解:(1)如图1,过点P作MN∥AE,
解:(1)如图1,过点P作MN∥AE,
∵MN∥AE(已作),
∴∠APM=∠A (两直线平行,内错角相等 ),
又∵AE∥CF,MN∥AE,
∴MN∥CF,
∴∠MPC=∠C(两直线平行,内错角相等 ),
∴∠APM+∠CPM=∠A+∠C,
即∠APC=∠A+∠C,
故答案为:A、C、两直线平行,内错角相等、两直线平行,内错角相等;
(2)如图2,∠AP1P2+∠P1P2C-∠A-∠C=180°,理由是:
过P1作P1B∥AE,过P2作P2G∥CF,
∵P1B∥AE,
∴∠BP1A=∠A,
∵P2G∥CF,
∴∠GP2C=∠C,
∵P1B∥AE,P2G∥CF,AE∥CF,
∴P1B∥P2G,
∴∠BP1P2+∠GP2P1=180°,
∴∠AP1P2+∠P1P2C=∠AP1B+∠BP1P2+∠P1P2G+∠GP2C=180°+∠A+∠C,
∴∠AP1P2+∠P1P2C-∠A-∠C=180°;
如图3,∠A+∠AP1P2+∠P1P2C-∠C=180°,理由是:
过P2作GP2∥CF,则∠GP2C=∠C,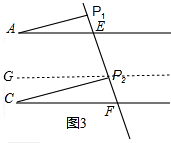
∵AE∥CF,
∴AE∥GP2,
∴∠AEF+∠GP2E=180°,
∵∠AEF=∠A+∠AP1P2,
∴∠AEF+∠P1P2C=180°+∠GP2C,
∴∠A+∠AP1P2+∠P1P2C=180°+∠C,
∴∠A+∠AP1P2+∠P1P2C-∠C=180°;
如图4,∠AP1P2+∠P1P2C-∠A+∠C=180°,理由是
过P1作P1G∥CF,则∠GP1F+∠CFP1=180°,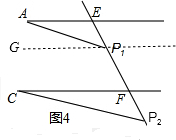
∵AE∥CF,
∴AE∥GP1,
∴∠A=∠AP1G,
∵∠EFC=∠C+∠P1P2C,
∴∠AP1P2+∠EFC=180°+∠AP1G,
∴∠AP1P2+∠C+∠P1P2C=180°+∠A,
∴∠AP1P2+∠P1P2C-∠A+∠C=180°.
故答案为:如图2,∠AP1P2+∠P1P2C-∠A-∠C=180°,如图3,∠A+∠AP1P2+∠P1P2C-∠C=180°,如图4,∠AP1P2+∠P1P2C-∠A+∠C=180°.
点评 本题考查了平行线的性质,辅助线的作出是本题的关键,属于典型题,作辅助线构建同旁内角互补,再利用外角定理和平行线的性质得出角的关系,相加或等量代换即可.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案| A. | x≠0 | B. | x>0 | C. | x≠1 | D. | x<1 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为( )| A. | x<-1 | B. | x>-1 | C. | x>2 | D. | x<2 |
| A. | 3x-2x=1 | B. | 2x+2x=2x2 | C. | (-x3)2=-x5 | D. | x•x=x2 |
 如图,在△ABC中,点I是两条平分线的交点.
如图,在△ABC中,点I是两条平分线的交点. 如图,在平面直角坐标系xOy中,菱形MNPQ的顶点P的坐标为(2,0),点N的坐标为(0,1),点M在第一象限,对角线NQ与x轴平行,直线y=x+8与x轴、y轴分别交于点A、B,将菱形MNPQ沿x轴向左平移k个单位,当点M落在△AOB内部时(不包括三角形的边),下列数据中不可能为k的值的是( )
如图,在平面直角坐标系xOy中,菱形MNPQ的顶点P的坐标为(2,0),点N的坐标为(0,1),点M在第一象限,对角线NQ与x轴平行,直线y=x+8与x轴、y轴分别交于点A、B,将菱形MNPQ沿x轴向左平移k个单位,当点M落在△AOB内部时(不包括三角形的边),下列数据中不可能为k的值的是( ) 已知,在△ABC中,∠C=90°,点D是AB上一点,DE⊥BC,垂足是点E,且BE=AC,若BD=$\frac{1}{2}$,DE+BC=1.求证:∠ABC=30°.
已知,在△ABC中,∠C=90°,点D是AB上一点,DE⊥BC,垂足是点E,且BE=AC,若BD=$\frac{1}{2}$,DE+BC=1.求证:∠ABC=30°. 如图,图锥的表面展开图由一扇形和一个圆组成,已知圆的周长为2π,扇形的圆心角为120°,则这个扇形的面积为3π(结果保留π)
如图,图锥的表面展开图由一扇形和一个圆组成,已知圆的周长为2π,扇形的圆心角为120°,则这个扇形的面积为3π(结果保留π)