题目内容
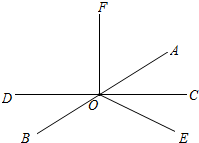 如图,已知过点O的直线AB平分∠EOF,直线CD与OF垂直,垂足为O.
如图,已知过点O的直线AB平分∠EOF,直线CD与OF垂直,垂足为O.(1)若∠EOF=116°,求∠AOC和∠BOE的度数.
(2)若钝角∠EOF的度数逐渐增大,那么∠AOC的度数如何变化?(直接写出结果)
考点:垂线,角平分线的定义
专题:
分析:(1)根据角平分线的性质,可得∠AOF的度数,根据角的和差,可得∠AOC,∠BOE的度数;
(2)根据角的和差,可得答案.
(2)根据角的和差,可得答案.
解答:解:(1)直线CD与OF垂直,得∠FOC=90°,
由直线AB平分∠EOF,得
∠AOF=∠AOE=
∠EOF=58°.
由角的和差,得
∠AOC=∠COF-∠AOF=90°-58°=32°,
∠BOE=180°-∠AOE=180°-58°=122°;
(2)若钝角∠EOF的度数逐渐增大,∠AOF增大,那么∠AOC的度数度数逐渐减小.
由直线AB平分∠EOF,得
∠AOF=∠AOE=
| 1 |
| 2 |
由角的和差,得
∠AOC=∠COF-∠AOF=90°-58°=32°,
∠BOE=180°-∠AOE=180°-58°=122°;
(2)若钝角∠EOF的度数逐渐增大,∠AOF增大,那么∠AOC的度数度数逐渐减小.
点评:本题考查了垂线,利用了垂线的定义,角的和差,角平分线的性质.

练习册系列答案
相关题目
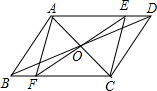 如图,在?ABCD中对角线AC、BD交于点O,并且∠DAC=60°,∠ADB=15°.点E是AD边上一个动点,延长EO交BC于点F,当点E从D点向A点移动过程中(点E与点D,A不重合),则四边形AFCE的变化是( )
如图,在?ABCD中对角线AC、BD交于点O,并且∠DAC=60°,∠ADB=15°.点E是AD边上一个动点,延长EO交BC于点F,当点E从D点向A点移动过程中(点E与点D,A不重合),则四边形AFCE的变化是( )| A、平行四边形→矩形→平行四边形→菱形→平行四边形 |
| B、平行四边形→菱形→平行四边形→矩形→平行四边形 |
| C、平行四边形→矩形→平行四边形→正方形→平行四边形 |
| D、平行四边形→矩形→菱形→正方形→平行四边形 |
下列计算正确的是( )
A、
| ||||||
B、
| ||||||
C、3
| ||||||
D、
|
 如图,在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
如图,在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.