Question

13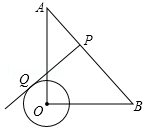．如图，在Rt△AOB中，OA=OB=4$\sqrt{2}$，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线长PQ的最小值为$\sqrt{15}$．

Answer 1

分析 连接OP，OQ，由PQ为圆O的切线，利用切线的性质得到OQ与PQ垂直，利用勾股定理列出关系式，由OP最小时，PQ最短，根据垂线段最短得到OP垂直于AB时最短，利用面积法求出此时OP的值，再利用勾股定理即可求出PQ的最短值．

解答 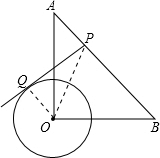解：连接OP、OQ，如图所示，
∵PQ是⊙O的切线，
∴OQ⊥PQ，
根据勾股定理知：PQ²=OP²-OQ²，
∴当PO⊥AB时，线段PQ最短，
∵在Rt△AOB中，OA=OB=4$\sqrt{2}$，
∴AB=$\sqrt{2}$OA=8，
∴S_△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OP，即OP=$\frac{OA•OB}{AB}$=4，
∴PQ=$\sqrt{O{P}^{2}-O{Q}^{2}}$=$\sqrt{15}$．
故答案为：$\sqrt{15}$

点评 此题考查了切线的性质，勾股定理，熟练掌握切线的性质是解本题的关键．