题目内容
1.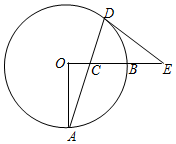 如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.(1)求证:∠ECD=∠EDC;
(2)若tanA=$\frac{1}{4}$,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
分析 (1)连结OD,根据等角的余角相等即可证明,只要证明∠ODA=∠OAD,∠EDC+∠ODA=90°,∠A+∠DCE=90°即可;
(2)由tanA=$\frac{OC}{OA}$,可知$\frac{OC}{8}=\frac{1}{4}$,推出OC=2,设DE=x,根据OD2+DE2=OE2,可得82+x 2=(2+x)2解方程即可;
(3)求两个弓形的面积之差即可;
解答  (1)证明:连结OD,
(1)证明:连结OD,
∵DE是⊙O的切线,
∴∠EDC+∠ODA=90°,
∵OA⊥OB,
∴∠ACO+∠A=90°,
∵OA=OD,
∴∠ODA=∠A,
∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,
∴∠ECD=∠EDC.
(2)解:∵tanA=$\frac{OC}{OA}$,
∴$\frac{OC}{8}=\frac{1}{4}$,
∴OC=2,
设DE=x,
∵∠ECD=∠EDC,
∴CE=x,
∴OE=2+x.
∴∠ODE=90°,
∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,
∴DE=CE=15.
(3)解:过点D作AO的垂线,交AO的延长于F,
当∠A=15°时,∠DOF=30°,DF=4,
${S_{弓形ABD}}=\frac{150π•64}{360}-\frac{1}{2}×8×4=\frac{80π}{3}-16$
当∠A=30°时,∠DOF=60°,DF=4$\sqrt{3}$,
${S_{弓形ABD}}=\frac{120π•64}{360}-\frac{1}{2}×8×4\sqrt{3}=\frac{64π}{3}-16\sqrt{3}$,
∴S=$(\frac{80π}{3}-16)-$$(\frac{64π}{3}-16\sqrt{3})=\frac{16}{3}π+16\sqrt{3}-16$
点评 本题考查圆综合题、切线的性质、等腰三角形的性质、勾股定理、弓形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

 如图,△ABC是等腰三角形,AB=AC=3,BC=1. 点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为( )
如图,△ABC是等腰三角形,AB=AC=3,BC=1. 点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | 1 |
| α | 30° | 45° | 60° |
| sinα | |||
| cosα | |||
| tanα |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{9}$ |
| A. | 0.201×10-4 | B. | 2.01×10-6 | C. | 20.1×10-6 | D. | 2.01×10-5 |
 如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).
如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示). 已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点.
已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点. 如图,E是?ABCD的边AD上任一点,若△EBC的面积为16,则?ABCD的面积为32.
如图,E是?ABCD的边AD上任一点,若△EBC的面积为16,则?ABCD的面积为32.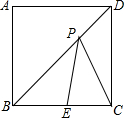 在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到$\sqrt{13}$.
在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到$\sqrt{13}$.