题目内容
15.在 Rt△ABC中,∠C=90°,且c=29,a=20,则b为( )| A. | 9 | B. | 10 | C. | 20 | D. | 21 |
分析 直接利用勾股定理得出b的值进而得出答案.
解答 解:∵∠C=90°,c=29,a=20,
∴b=$\sqrt{2{9}^{2}-2{0}^{2}}$=21.
故选:D.
点评 此题主要考查了勾股定理,正确计算是解题关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
5.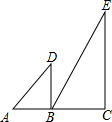 如图,在直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°,若将△ABD绕点B按顺时针方向旋转,当AD∥BC时,旋转的角度是( )
如图,在直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°,若将△ABD绕点B按顺时针方向旋转,当AD∥BC时,旋转的角度是( )
 如图,在直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°,若将△ABD绕点B按顺时针方向旋转,当AD∥BC时,旋转的角度是( )
如图,在直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°,若将△ABD绕点B按顺时针方向旋转,当AD∥BC时,旋转的角度是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
10. 如图所示,在等腰直角△ABC中,∠B=90°,将△ABC绕点 A逆时针旋转60°后得到的△AB′C′,则∠BAC′等于( )
如图所示,在等腰直角△ABC中,∠B=90°,将△ABC绕点 A逆时针旋转60°后得到的△AB′C′,则∠BAC′等于( )
 如图所示,在等腰直角△ABC中,∠B=90°,将△ABC绕点 A逆时针旋转60°后得到的△AB′C′,则∠BAC′等于( )
如图所示,在等腰直角△ABC中,∠B=90°,将△ABC绕点 A逆时针旋转60°后得到的△AB′C′,则∠BAC′等于( )| A. | 105° | B. | 120° | C. | 135° | D. | 150° |
20.单项式-$\frac{{2}^{2}x{y}^{2}}{5}$ 的次数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
7. 下列四个水平放置的几何体中,三视图如图所示的是( )
下列四个水平放置的几何体中,三视图如图所示的是( )
 下列四个水平放置的几何体中,三视图如图所示的是( )
下列四个水平放置的几何体中,三视图如图所示的是( )| A. |  立方体 | B. |  三棱柱 | C. |  圆柱 | D. |  长方体 |
5.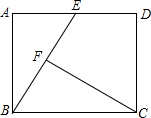 如图,在矩形ABCD中,E是AD边的中点,CF⊥BE,垂足为点F,若BF=EF,AE=1,则AB边的长为( )
如图,在矩形ABCD中,E是AD边的中点,CF⊥BE,垂足为点F,若BF=EF,AE=1,则AB边的长为( )
 如图,在矩形ABCD中,E是AD边的中点,CF⊥BE,垂足为点F,若BF=EF,AE=1,则AB边的长为( )
如图,在矩形ABCD中,E是AD边的中点,CF⊥BE,垂足为点F,若BF=EF,AE=1,则AB边的长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 如图,AB∥CD,∠C=20°,∠E=25°.则∠A=45°.
如图,AB∥CD,∠C=20°,∠E=25°.则∠A=45°.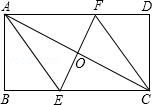 将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,