题目内容
5．
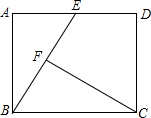如图，在矩形ABCD中，E是AD边的中点，CF⊥BE，垂足为点F，若BF=EF，AE=1，则AB边的长为（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
分析 直接利用线段垂直平分线的性质得出EC=BC，再利用矩形的性质结合勾股定理得出AB的长．
解答 
解：连接EC，
∵CF⊥BE，垂足为点F，BF=EF，
∴BC=EC，
∵E是AD边的中点，AE=1，
∴AE=ED=1，
∴BC=AD=2，
∴AB=DC=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$．
故选：C．
点评 此题主要考查了矩形的性质以及勾股定理、线段垂直平分线的性质等知识，正确得出EC的长是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
15．在 Rt△ABC中，∠C=90°，且c=29，a=20，则b为（ ）
| A． | 9 | B． | 10 | C． | 20 | D． | 21 |
16．
甲、乙两人在操场上赛跑，他们赛跑的路程S（m）与时间（min）间的函数关系如图所示，则下列说法中正确的个数有（ ）
①甲、乙两人进行1000米赛跑②甲先慢后快，乙先快后慢③比赛到2分钟时，甲、乙两人跑过的路程相等④甲、乙同时到达终点．
甲、乙两人在操场上赛跑，他们赛跑的路程S（m）与时间（min）间的函数关系如图所示，则下列说法中正确的个数有（ ）①甲、乙两人进行1000米赛跑②甲先慢后快，乙先快后慢③比赛到2分钟时，甲、乙两人跑过的路程相等④甲、乙同时到达终点．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
20．下列各数中是有理数的是（ ）
| A． | π | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
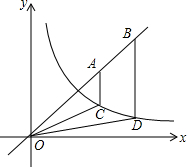如图，点A，B为直线y=x上的两点，过A，B两点分别作y轴的平行线交双曲线y=$\frac{1}{x}$（x＞0）于C，D两点，若2BD=5AC，则OC2-$\frac{4}{25}$OD2的值为$\frac{42}{25}$．