题目内容
19.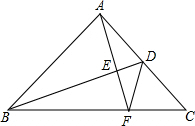 如图,已知BD是等腰Rt△ABC腰上的中线,AE⊥BD于点E,AE的延长线交BC于点F,连接DF,求证:∠ADB=∠CDF.
如图,已知BD是等腰Rt△ABC腰上的中线,AE⊥BD于点E,AE的延长线交BC于点F,连接DF,求证:∠ADB=∠CDF.
分析 由∠BAC为直角,得到其它两锐角互余,又根据AE与BD垂直,得到三角形ADF为直角三角形,故两锐角也互余,根据同角的余角相等即可得证.
解答 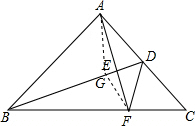 证明:作AG平分∠BAC,交BD于点G
证明:作AG平分∠BAC,交BD于点G
∵∠BAC=90°,AE⊥BD,
∴∠DAE+∠ADB=∠ABE+∠ADB=90°,
∴∠ABG=∠CAF,
∵△ABC是等腰直角三角形,
∴AB=AC,∠C=∠BAG=45°,
在△BAG和△CAF中,
$\left\{\begin{array}{l}{∠ABG=∠CAF}\\{AB=AC}\\{∠C=∠BAG=45°}\end{array}\right.$,
∴△BAG≌△CAF(ASA),
∴AG=CF,
在△AGD和△DFC中,
$\left\{\begin{array}{l}{AG=FG}\\{∠GAD=∠C}\\{AD=CD}\end{array}\right.$,
∴△AGD≌△DFC(SAS),
∴∠ADB=∠CDF.
点评 本题考查了等腰直角三角形的性质以及全等三角形的判定与性质.添加合适的辅助线,构造全等三角形是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.南海是我们固有领土,南海资源丰富,其面积约为350万平方千米,相当于我国的渤海、黄海和东海总面积的3倍,其中350万用科学记数法表示为( )
| A. | 3.5×106 | B. | 3.5×107 | C. | 0.35×108 | D. | 3.5×109 |
8.已知直线y=2x+k(k为常数且不为0)不经过第二象限,则双曲线y=$\frac{k}{x}$一定经过的象限是( )
| A. | 一、三 | B. | 二、四 | C. | 三、四 | D. | 一、二 |
9.地球半径约为6 400 000米,这个数用科学记数法表示为( )
| A. | 640×104 | B. | 64×105 | C. | 6.4×106 | D. | 0.64×107 |
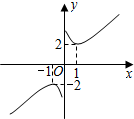 已知函数y=x+x-1,其图象如图.给出下列几个命题:①该函数的图象是中心对称图形;②y的值不可能为1;③当x<0时,该函数在x=-1时取得最大值-2;④在每个象限内,函数值y随自变量x的增大而增大.其中正确的个数是( )
已知函数y=x+x-1,其图象如图.给出下列几个命题:①该函数的图象是中心对称图形;②y的值不可能为1;③当x<0时,该函数在x=-1时取得最大值-2;④在每个象限内,函数值y随自变量x的增大而增大.其中正确的个数是( )
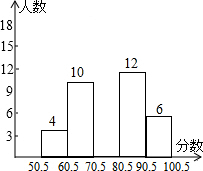 某班数学期末考试后,班主任将所得的成绩(分数取整数)进行整理分成5组,并绘成频数分布直方图(如图),已知70.5~80.5分数段的频率为0.36,请结合直方图提供的信息,解答以下问题:
某班数学期末考试后,班主任将所得的成绩(分数取整数)进行整理分成5组,并绘成频数分布直方图(如图),已知70.5~80.5分数段的频率为0.36,请结合直方图提供的信息,解答以下问题: