题目内容
12. 如图,在平面直角坐标系中,点P(3a,a)是反比例函y=$\frac{12}{x}$与⊙O的一个交点,则图中阴影部分的面积为10π.
如图,在平面直角坐标系中,点P(3a,a)是反比例函y=$\frac{12}{x}$与⊙O的一个交点,则图中阴影部分的面积为10π.
分析 先利用反比例函数解析式y=$\frac{12}{x}$确定P点坐标为(6,2),由于圆心在原点O,则圆的面积的面积为40π,然后根据反比例函数图象关于原点中心对称得到阴影部分的面积为圆面积的$\frac{1}{4}$.
解答 解:把P(3a,a)代入y=$\frac{12}{x}$得3a•a=12,解得a=2或-2,
∵点P在第一象限,
∴a=2,
∴P点坐标为(6,2),
∴OP2=62+22=40,
∴圆的面积=40π,
∴图中阴影部分的面积=$\frac{1}{4}$S圆=10π.
故答案为10π.
点评 本题考查了反比例函数图象的对称性:反比例函数图象既是轴对称图形又是中心对称图形,对称轴分别是:①二、四象限的角平分线y=-x;②一、三象限的角平分线y=x;对称中心是:坐标原点.

练习册系列答案
相关题目
20.下列方程中,是一元一次方程的是( )
| A. | 3x+y=5 | B. | y2=1 | C. | $\frac{1}{x}$=3 | D. | 3x+2=4x-7 |
7.在坐标系中,以原点为圆心,以5为半径画圆,则点A(-3,4)的在( )
| A. | 圆内 | B. | 圆上 | C. | 圆外 | D. | 不能确定 |
2.不等式-3(x+2)>a+2的解是负数,则a的取值范围是( )
| A. | a≥-3 | B. | a≥-10 | C. | a≥-8 | D. | a<0 |
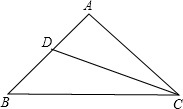 如图,△ABC中,∠A=90°,CD平分∠ACB,若AD=1,AC=2,BC=$\frac{10}{3}$,求△ABC的面积.
如图,△ABC中,∠A=90°,CD平分∠ACB,若AD=1,AC=2,BC=$\frac{10}{3}$,求△ABC的面积.